The preliminaries we cover in this lecture are just that: preliminaries. They are the things you should know already, either from prior courses you've followed, or from your high school education. However, since this course caters to many programs, we cannot fully ensure that all the preliminaries have been perfectly covered in all cases. This lecture describes and explains the basics. If you've never seen this material before, this treatment is probably too brief to get a deep understanding.
Think of this as a recap: if there's anything in this lecture you've never seen before, make sure to take some time to dig into it a little deeper. If you ever get stuck at any point in the course, it may be that there are some preliminaries you didn't quite cover.
If you basically know this stuff already, feel free to get started with the lectures, and see how far you get. We try to start slow, and gently ramp up the complexity as the course progresses. With a bit of luck, every step is just enough preparation for the next. If not, and you get stuck on a particularly hairy bit of math, remember that you can always come back here. Perhaps another look at the basic properties of these fundamentals can help you to see what we're doing.
Before we get started, a note on what it means to "understand" a mathematical topic. To illustrate, here is a controversial quote from mathematician John von Neumann.
Many math teachers hate this quote, because it implies something about rote learning over intuitive understanding. However, von Neumann was no idiot, and there is certainly a deep truth to this statement.
For me, the key principle he's getting at is the difference between understanding the principle of something and being thoroughly familiar with it, to the extent that you can even use it without conscious effort. As a metaphor, imagine a musical score (i.e. sheet music). I had some lessons as a child, so I understand the principle of sheet music entirely. With some time I can find any note indicated in the score. What I cannot do is sight read: look at a score and play it directly, or hear in my head what it sounds like. That takes more than understanding: it takes practice.
The same is true for mathematics. You probably understand the ideas of logarithms and sums pretty well already, and after this lecture hopefully a little better. However, to really follow along with complex derivations, you'll need to get so familiar with them that they feel like second nature: like reading, or typing on a keyboard: the sort of thing you can do while concentrating on something else.
When learning mathematics, sometimes you understand first and then you slowly “get used to”. Sometimes it's the other way around, and you need to take something you don't fully understand, and play around with it. The more you get used to it, the more you feel like you understand.
To sufficiently "get used" to certain concepts, your need to practice enough to work them into your muscle memory. For all the concepts discussed in this lecture, that is required if you really want to understand machine learning, and we offer some exercises to help you do that.
Here is an example of a particularly complex derivation that will come up in one of the later lectures. Without the required context it will be impossible to understand what this is about, or what we're doing here. Don't worry about that. The reason we show this here is to emphasize that even though this looks very complicated, it's using only a few very basic mechanisms that you should be familiar with already:
Sum (capital sigma) notation
Logarithms
Expectations
(Conditional) probabilities
Even if you don't understand what this is about, the basic properties of the above four concepts should be enough to tell you how every line follows from the previous.
Don't worry if that's too much at the moment, we'll work up to this level of complexity step by step. However this hopefully indicates that it's crucial to not just understand these four concepts but to really get used to them, in the sense of von Neumann. If you do that for the topics covered in this lecture, you should be able to follow along, even with very complex derivations like these.
In this lecture, we'll go over some of the mathematical preliminaries. The stuff you should know before you start doing machine learning.
In the first section, we will deal with three different mathematical topics that come up a lot. They are not complicated, but you’ll need to get very familiar with them to read basic machine learning material. Even if you know them already, it pays to practice, so that you get used to them.
Here is the basic idea of the logarithm. It's simply the inverse of the the exponent function. If 64 is 2 raised to the power of x, what is x? It’s log2(64) = 6, because 26 = 64.
This doesn’t, however, go very far towards explaining why the logarithm is so special.
In fact you may not even think of something so simple as an inverse function to require "invention". And yet the invention of the logarithm (or perhaps the method of logarithms is more accurate) by John Napier was a great watershed for the natural sciences.
This quote (from a book on navigation in from 1958) refers to a small book that Napier published containing simple tables of logarithms. This was a watershed because it allowed people to quickly compute things that would have been terribly laborious before.
The fundamental reason for this is that logarithms turn multiplications, which are complex and laborious to perform without a computer, into additions, which are a much simpler business.
Here is why that is the case. Imagine that we have three positive numbers a, b and c, for which we know that ab = c.
The trick behind logarithms is that we can choose to refer to a, b and c simply by different names. We know that there must be some number x such that 2x = a. Whatever that number is, we call it x, and we create similar numbers y and z to refer to b and c.
How does the knowledge that ab = c translate to this new set of names for our numbers? Filling in the multiplication, we get 2x2y = 2z. Now, It is a basic property of exponentiation that 2x2y = 2x+y.
That is, with our new names, the multiplication has become a sum. By summing x and y, we find the number z, and z is the new name of the number c that we wanted to compute.
This is why Napier is so famous (at least in certain circles). If you have some horrendous multiplication to compute, all you have to do is rename your numbers. After the renaming, you can sum them and you get a solution for your multiplication in the renamed form, for which you can then look up the original name. The renaming back and forth is what Napier's "little book" allowed people to do: all they had to do was look up the right numbers in a table.
The renaming function that creates these well-behaved numbers is the logarithm. We've used base-2 logarithms here, but any other base would do just as well.
This principle is how people could calculate quickly before computers became commonplace. First by using large pre-computed tables of logarithms, and then by using slide rules. The idea is that it's very easy to use the sliding action of two rulers to mimic a summation. If you then label the rules with logarithms rather than linearly spaced numbers, you can use the slide rule to "look up" multiplications.
Image source: https://commons.wikimedia.org/wiki/Category:Slide_rules#/media/File:Slide_Rule_(PSF).png
Another way to think of the logarithm is as indicating the number of digits you'll need to write a number down. The slide shows an example: for each of these numbers, if we take the base ten logarithm and round it up, we get the number of digits.
Why should this be the case? Ask yourself how many numbers you can write down with three digits. There are ten options for the first digit, ten for the second and ten for the third, so the answer is 10 · 10 · 10 = 103. That is, the first number that you can't write down with three digits is exactly 103. The same reasoning holds for any number of digits: the first number that you can't write down with n digits is 10n. Or, put differently if a number is smaller than 10n, you can write it down in n digits or fewer. The function floor(log10(x)+1) gives us the first integer n such that x is smaller than 10n. In other words, the number of digits we need to write down x.
This provides a natural interpretation to the "multiplication to sum" property of logarithms. Imagine the multiplication of 100000 (105) by 1000 (103). Despite these being very large numbers, the multiplication is easy to do. We just add the zeroes of the second number to those of the first. The length of the result, written down in Arabic numerals is roughly the length of the first number plus the length of the second number. This is roughly true for any multiplication, if we count the length as the logarithm of a number.
You can also use this to provide crucial interpretation for the binary logarithm log2. When we asked how many different numbers you can write with three digits, 10·10·10, we used the fact that there are exactly 10 digits. What if we didn't have ten symbols but only 2? Say, 0 and 1. In such a situation we could represent only two numbers with such a "two-digit" after which we would need to add more to represent a third number. With three of such two-digits, we could represent 2·2·2 = 23 numbers. Two-digits of course, are called bits. The binary logarithm of x indicates how many bits we need to represent x (by the same formula as above).
Here are the most important properties of the logarithm to remember. These are the main things you'll need to work into your muscle memory.
For the last property, we've given a little proof to show how it follows from the previous two properties.
One final base that we'll often use for our logarithms is e ≈ 2.1718... . This is because the function ex is a particularly special one. We can show why this function is special later in the course. For now, just remember that this is one particular base we will often use.
Ok, so that's why logarithms are historically important. Why do we still use them so much nowadays? We have calculators aplenty to multiply numbers for us, so why put logarithms front and center among our preliminaries?
There are two reasons. The first is in analysis. When we are analysing our formulas and algorithms, we deal with a lot of complicated expressions. Here is an example: the famous normal distribution. Its probability likelihood curve looks like this. It's defined by the complicated formula on the left (this normal function has mean 0 and variance 1).
The only thing we need to worry about now is that it's positive everywhere, so we can take its logarithm. This changes the function, but in a very predictable way: for instance, because the logarithm only ever increases, that means that whereever the normal function increases, so does its logarithm. This means that, for example, the peak is in the same place for both functions.
So, if we start with the complicated function on the left, and take its (natural) logarithm, we end up with the function on the left. See if you can show this with the properties from the previous slide, it's good practice.
In "log space" the function still has some complicated bits, like the part in gray, but we can note that these do not depend on x. It's just some number. That means that this logarithmic function is just a simple parabola: the most complicated part is just the square of x. Parabolas should be much more familiar to you than the complicated function on the left.
This is the first reason to use logarithms. For many of the functions we will want to analyse, taking their logarithm retains the important properties, but simplifies their expression.
The other reason we use logarithms often is for numerical precision. In the platonic ideal of mathematical thought, we don't need to worry about this. We can imagine a number that is arbitrarily small, for instance, as close to zero as we like. Even if it would take billions of 0's to write it as 0.0000....000000001, we can still imagine it.
When we actually want to compute with a number like that, things don't work quite so neatly. Try and put this number in a computer (using the standard so-called floating point representation), and the computer essentially won't have room for that many zeros. The result is that the number becomes 0. We call this an underflow.
This is especially problematic if you want to deal with large products of potentially small probabilities. Imagine for instance that you pick a random word from a random wikipedia article. The probability of seeing the word the is 0.1 and the probability of seeing the word cat is 0.01.
You repeat the experiment a few times. Which is more likely, seeing the word the 400 times in a row, or seeing the word cat 300 times in a row? Let's ask python. To do so, we just multiply the value 0.1 by itself 400 times, and 0.01 by itself 300 times.
Sadly, python thinks both probabilities are 0, we cannot compare them. They aren't zero, it's just that the smallest number that the python representation can handle is about 10-323. Smaller than that, and we underflow.
For this reason, we almost never store raw probabilities like these. Instead, we store the logarithms of probabilities. We'll use base 10 here, for clarity, but any base would do. With these numbers, we can compute the log probability of seeing "the" 400 times in a row and seeing "cat" 300 times in a row. All we need to do is add where we would normally multiply, so we add -1 to itself 400 times and we add -2 to itself 300 times. This gives us the log probability of seeing the 400 times (-400) and the log probability of seeing cat 300 times (-600). Because the logarithm is monotonically increasing we know that when log x is smaller than log y, x is also smaller than y (i.e. 10-400 > 10-600) From this we can get our answer.
Another topic you should make sure you get used to is sum notation. You've probably seen it a few times before already: it's the big capital letter Sigma (the greek s, for "sum").
It works as follows: whenever you have a sum with many terms, you figure out if you can write a single expression that shows what each term looks like. For instance, if we have a sequence of numbers (a1, a2, a3) which we want to sum, a1 + a2 + a3, then we can write each term in this sum as ai, where the variable i takes the value i=1, i=2 or i=3.
The sigma notation allows us to express a sum like this. Below the sigma, we define the starting value for i, and above it, we define the final value. Then, to the right, we define what each term looks like when phrased in terms of i.
Of course, for this example, the explicit sum looks much simpler, and easier to understand. This is an important point to understand: we don't just write things in sigma notation because it looks more fancy. There are very advanced math books that almost never touch the sigma notation, and write all their sums explicitly, and they are much clearer for it.
However, as sums get more complex, this balance may shift: some formulas look much clearer in sigma notation. Especially those that have an arbitrary number of terms, or even an infinite number of terms. This is the case in machine learning, and you will see a lot of sigmas in our research papers and textbooks.
Here's an example you'll see a lot in the course: computing the average (or mean) of a bunch of numbers.
Imagine we have a small group of 5 students, who have all received a grade on an exam. We name the students 1, 2, 3, 4, and 5, and we name their grades s1, s2, s3, s4 and s5. You hopefully know how to compute the average of a set of numbers: sum them all up, and divide by how many there are. We can write that as an explicit sum, but we can also write it in the sigma notation.
The second example shows one of the benefits of the sigma notation: the formula doesn't change much if we don't know how many students we have. We just replace 5 by n. And everything stays the same.
Here are some simple examples for you to test your understanding on.
In order to get properly used to sum notation, it's important to internalize the following rules. They follow very clearly from what you know already about regular sums, so they shouldn't be very surprising. In practice, to follow a derivation, you'll often need to do something like identifying a constant factor inside the sigma, and take it outside, as the first rule lets you do. Or, to take a constant inside the sum applying the rule in reverse order.
It's important to note that the sum notation can be a little ambiguous. Like here: is the second sigma "inside" the first, or outside?
That is, do we first sum the a's,and then the b's and then sum these together? Or do we take the sum of b and add it to every element of a before summing these? The sum notation doesn't specify. If a sum is written like this, both could be true. Hopefully the context provides sufficient hints to figure out what is going on.
Often, we prefer the ambiguity to the extra brackets if it's clear from context what we mean. In many cases, however, you can avoid both the brackets and the ambiguity by cleverly arranging your formula.
For people who are more comfortable with programming than with math, it can often be helpful to think of sum notation as a kind of mathematical notation for a for-loop.
If this works for you, it can be a great shortcut to get comfortable with this kind of notation. However, you should note that while the two are similar, they actually express fundamentally different things. A sum is simply a mathematical quantity to refer to, while a program is a set of instructions for computing that quantity. A sum can have infinitely many terms, or terms that are incomputable, and yet the sum remains a perfectly viable statement, even if the corresponding for loop becomes nonsense
In short, it can be very helpful to translate mathematical statements to computer programs, to help you understand them, but you must always keep in the back of your mind that they are not the same thing.
Here are some variations of the sum notation that you are likely to encounter. From left to right:
Summing over sets. If you want to sum over the elements of a set, you only need to indicate what set you are getting your elements from and what you'll call those elements. That looks like it does on the left. Note that you don't need to specify in which order you are getting the elements from the set, since the value of the sum is the same in whatever order you sum the elements together.
Simplified sum notation. Let's be honest: the full sum notation is a hairy beast. It looks intimidating and it's difficult to parse. More often than not, it's perfectly clear from context what the starting point and end point are. In such case, all you really need to do is to specify which letter indicates how the formula on the right changes from term to term.
Infinite sums. One particularly powerful option of the sum notation is to write infinite sums. We do this by simply replacing the top element by an infinity symbol. This doesn't always mean that the sum itself becomes infinite as well. For instance, the value of the sum you see here is 1.
Here's a little illustration of how an infinite sum can have a finite value (if you've never seen that before).
The square with sides of 1x1 has area 1. The first term (1/2) corresponds to a rectangle with proportions 2:1 that fills half the square, leaving another rectangle of the same size. The next term corresponds to half that, so we can cut the remaining rectangle into two equal squares: one corresponding to the next term and one corresponding to the remainder. The remainder is a square the same size as the previous square. We can cut another rectangle corresponding to the next term, leaving another rectangle of the same size. We can continue this forever: whenever the remainder is a square, we cut it into two rectangles, and whenever it's a rectangle we cut it into two squares.
In the limit, we get closer and closer to filling the entire square.
NB. Slides like these, with gray headers are slides that contain non-essential stuff. You can skip them if you're in a hurry, but if you have time, working through examples like these can be just the thing to help you to get to grips with the material.
The final thing we need to get used to is the argmax and argmin notation. This is used to define where functions have their highest and lowest values.
The slide illustrates the basic idea of the notation. Below the “argmax” we write the variable for which we want to find the value, and to the right of it we write the function that we want to maximize.
Here is a simple example. The function -x2 + 1 is a parabola. It’s shaped like a “bump” and trails off to negative infinity on both sides of the bump. This means that the highest value we can get out of the function is at the peak of the bump. This happens at x=0, at which point we have f(x) = 1. Thus, 0 is the result of the argmax.
Note: not 1, but 0. The argmax returns the location of the maximum, not the value.
Argmin works exactly the same way as argmax, except that we are looking for the minimum of the function: that is, we want the value of x for which x2 + 1 is at its lowest.
Note that we had to change the function to illustrate argmin. The first function we used doesn’t have a minimum: however low the value of -x2 + 1 is for some x that you’ve chosen, we can always find another x with a lower f(x). The takeaway is that it depends on the function whether or not the argmin or argmax returns a meaningful result.
If you are more comfortable reading code than math, you could again compare the mathematical notation to a snippet of code that does a similar thing.
In this case, however, you should note that there is a more substantial difference between the code and the math. The mathematical expression provides the argmax over all real values that x can take from negative infinity to positive infinity. The code code can only ever check a finite number of values. Even if we’re sure that the answer is somewhere between 0 and 100, we need to take a finite number of steps between those two values. In between, say, 1 and 1.1, there are infinitely many values that we should check if we really want the answer.
In short, the code provides a naive approach to finding an approximate answer. The mathematical definition points to the perfect solution, but doesn’t tell us how to calculate it.
We will often write derivations, where we turn one argmax, the one we’re interested in, into another one, which is easier to analyze. For this, we usually use two basic rules. Both rules apply to argmax and argmin in the same way.
First, the argmax of f(x), is the argmin of - f(x). This is because sticking a minus in front of a function essentially flips in the whole function around the horizontal axis. That means any maximum becomes a minimum.
The second rule holds when we feed f(x) to any function which is monotonically increasing. That’s a fancy way of saying that if the input gets bigger, the output always gets bigger as well. One example is the logarithm: if we make the input y a little bigger, the output log(y) will also get a little bigger, no matter what value y was originally (so long as it’s not negative, where the logarithm becomes undefined).
This means that the maximum of f(x) is in the same place as the maximum of log f(x).
The final line shows another example of this rule. If c is a constant, then the function c·y is monotically increasing, so we can always multiply the inside of the argmax/min by a positive constant without changing the answer. If c is a negative constant, all we need to do is apply the first rule to turn it into a positive constant.
Here is an example derivation.
See if you can tell, for every line of the derivation, which rule we’ve applied. If you draw the graph of the absolute function, you will be able to see why the last line is correct.
In this part we'll discuss the basics of linear algebra. For our purposes, linear algebra is just a convenient way of talking about lists and tables (or grids) of numbers. Machine learning deals with data, which often comes in the form of a list or a table of numbers, and linear algebra allows us to represent and manipulate these efficiently.
These are the topics we'll briefly discuss. As before, this is just the tip of the iceberg, but hopefully just enough to understand what's coming.
Pay particular attention to the slides about the dot product. That is going to come up a lot.
Let's start with vectors. A vector is a list of numbers. That's all. There's a lot we can do with vectors, and a lot of meaning we can assign to it, but for our purposes, all a vector is at heart is a simple list of numbers.
When we refer to a vector we will use a bold lowercase letter, like x here.
How many numbers there are in a vector (in this case 3), is called its dimension or dimensionality. Usually, we need vectors to have the same dimension for them to meaningfully interact with one another.
The reason for this name is that a vector with dimension n can represent a point in an n-dimensional space. In the slide, we have a 3 dimensional space. To find the point that the vector (2,4, 1) represents, we take two steps along the first axis, 4 steps along the second and 1 along the third.
We also use vectors to represent arrows in this space. Arrows have a direction and a magnitude (the length of the arrow). This makes them useful for many things: for instance to represent the speed of something. If you're driving a car, your speed has a certain magnitude (say 80 km/h), but it also has a direction (hopefully the direction of the road). We can represent both with a single arrow.
When we use vectors to represent an arrow, the convention is that we are talking about the arrow from the origin (0, 0, 0) to the point represented by the vector. That is, every arrow represented by a single vector starts at the origin.
When we want to refer to a specific element of a vector, we put the index of that element in the subscript, and use a non-bold letter for the vector. For instance x2 = 4.
Vectors are used to represent many different things in machine learning, but to make things a bit more concrete, here is one example. In machine learning we deal with instances: examples of some sort of thing we're trying to learn about. For example, we might be trying to learn about employees of a construction company. If we represent each employee with three numbers: their productivity on a scale from 0 to 1, the number of sick days they've take this year, and their age, then every employee in our company becomes one vector of dimension 3.
The set of all employees then becomes a cloud of points in a 3 dimensional space.
The simplest way to compute with vectors is to use element-wise operations. Whenever two vectors have the same dimension, we can make a third vector by, for instance, adding every element from the first to the corresponding element of the second. Or by multiplying, subtracting or dividing these elements.
This is called element-wise addition, element-wise multiplication, and so on. For every operation that takes to numbers and produces a third, we can also apply it element-wise to two vectors of the same length.
Vector addition is a particularly important element-wise operation on vectors. We can easily visualize what happens when we add two vectors a and b: we take the base of the arrow of b and place it at the tip of the arrow of a. The tip of this shifted copy of b is then the tip of the arrow of a + b.
This also gives us a very natural way to think of vector subtraction. When a, b, and c are numbers then c - b is the number a such that a + b =c.
For vectors c - b is the vector a such that a + b = c. That is, the vector we need to add onto the end of b, in order to get to c.
The length or magnitude of a vector (not to be confused with its dimension) is the length of the arrow it represents. That is, the distance between the origin and the point it represents.
We write the length of x, also known as its Euclidean norm, as ||x||.
In 2 dimensions, this value is given very simply by the pythagorean theorem. The value of the first element x1, the second element x2 and the arrow the vector represents together form a right-angled triangle. Thus, by Pythagoras, we have ||x||2 = x12 + x22. Taking the square to the other side, we see that the length is the square root of the sum of the squares of the individual elements.
This idea generalizes to vectors of higher dimension in a natural way: the square of the length is the sum of the the squares of the individual elements.

The length of a vector often comes in when we need to normalize a vector. That is, we want to keep it pointing in the same direction, but other change its length to be equal to one 1 (either by shrinking or expanding it as the case may be).
The operation that achieves this, is to divide each element of the vector x by the vector's norm ||x||. You can prove this algebraically by starting with the norm of this new vector, ||(x/||x||)||, filling in the definitions, and rewriting until you get the answer 1. This is a good exercise to get comfortable with the notation, and we suggest you try, but it isn't very intuitive.
The intuitive explanation for why this is the case, is a fundamental principle of geometry: if you draw a picture and uniformly scale it, the the lengths of all line segments in the picture are scaled by the same factor. That is if you make any picture half as wide and half as high, all distances in the picture will be half of what they were before.
In this case, we can image the picture being defined by the components of x: how far they extend along each axis. When we scale these so that x becomes x/||x||, all line segments are scaled by the same factor, including the line segment from the origin to the tip of x. Since its length was ||x|| before, and we scale it by 1/||x||, it must be 1 now.
We can now express the distance between two vectors a and b simply as the norm of the vector c that stretches from the tip of a to the tip of b, or: ||a - b||. The square of the distance has a particularly neat expression (and is used as often as the distance itself).
The distance between two vectors is one way to measure how similar they are. But there is another measure of similarity that we tend to use a lot more…
We call this operation the dot product. It takes two vectors of the same dimension, and returns a single number (like the distance). It is computed very simply by element-wise multiplying the two vectors and then summing the result over all elements.
It's hard to overstate quite how crucial the dot product is. It's going to come back a lot. Honestly, the majority of modern machine learning is built on just the basic properties of this one simple function one way or another.
Given that, let's take some time to really dig deep into the dot product. Let's look at various intuitions and definitions.
One way to think of the dot product is as an expression of how similar one vector is to another. In machine learning we often have multiple instances that we compare to a template.
Imagine, for instance that you want to hire somebody for a job. You set a few criteria you want to evaluate on: how friendly somebody is, how efficient somebody is and how risk-averse somebody is. You represent what you want with a vector of three dimensions. If you want somebody who is very friendly, you set the first value to a high positive value, and if you want somebody who is very unfriendly (perhaps you are looking for a bouncer or a bodyguard) you set it to a high negative value. If you don't really care, you set it to a value near 0. You do the same for the other two attributes.
Then, you represent each candidate with such a vector as well: if they are very friendly, the first element is high and positive, if they are unfriendly it is high and negative, and if they are neither, it is somewhere near zero.
We can now take a given candidate and take the dot product with the template to see how well they match.
Look at the first term. Imagine that you are looking for a very unfriendly person. In that case the first element of t is a large negative number. If the candidate is very friendly, the first element of c is a large positive number. Multiplying the two together, we see that the first term of the dot product is large and negative, so this particular mismatch in attributes results in a large lowering of the dot product. If the two had matched, we would have a high positive first term.
What if you don't really care about friendliness? Well, then t1 is close to zero, so whatever the value of c1, the first term is (relatively) close to zero as well, and the term does not contribute much to the dot product.
Here are some basic properties of the dot product. You should study each carefully to see if you understand what it means, and how you can derive it from the definitions we have given so far.
In the third line, 0 stands for the vector filled with zeros.
In the property of homogeneity c represents a scalar value (i.e. a number not a vector). Multiplying a vector by a scalar is done simply by multiplying each element by that scalar.
Pay particular attention to the property of distributivity. We'll come back to that one.
One remarkable feature of the dot product is that it can also be expressed with an entirely different formula, which at first sight has nothing to do with the definition we just gave. We call this the geometric definition, and the earlier version the algebraic definition.
The geometric definition states that the dot product xTy is also the product of the lengths of x and y and the cosine of the angle between them.
We’ll first look at some of the consequences of this definition, and then show that the two are equivalent.
Before we look into how to get from one definition to another, let's see how this definition chimes with the intuition we already have. We'll return to the example of finding candidates for a job, but we'll stick to just the first two properties, so we can easily plot the resulting vectors.
This gives us an idea of how the similarity work geometrically. Candidate 2 is pointing in the exact opposite direction of our template. This makes the angle between the two vectors as big as possible, giving us a cosine of -1, leading to a large , negative dot product. The more we pivot the candidate vector towards the template, the closer we get to a cosine of 1, giving us the maximal dot product.
From this definition, we can look back to our list of properties and see what they mean with the geometric picture in mind. Some of them now become a lot simpler to show, some less so. Distributivity, in particular, is a lot easier to prove with the former definition.
We can also add one more property, which is almost impossible to see with the first definition. If neither a nor b is the zero vector, then the only way their dot product can be zero is if the angle between them is 90 degrees. That is they are orthogonal to one another.
This may seem a fairly arbitrary fact, but when we use the dot product to measure similarity between vectors, an angle of 90 degrees in a way represents the lowest similarity. Orthogonal eigenvectors represent things that have nothing to do with each other. This represents a kind of independence.
On the previous slide we compared candidates to instances. You may think that the candidate that pointed in the exact opposite direction to the template was the least similar. And that's a fair point, but in many ways they are still related. The candidate is the unique opposite of the template. An orthogonal vector is more like the "most unrelated" vector possible.
One final view of the dot product is that it expresses the projection of one vector onto another. Projections are extremely important in many areas of linear algebra, especially in the ones related to machine learning. This is because they define how close you can get to some target while being constrained to some subspace.
For example, ask yourself how close you can get to the tip of a, while staying on the line of b (its arrow extended in both directions). The answer is given by the point where the line between your chosen point on b and the tip of a makes a right angle with b. This is called the projection of a onto b (which we'll denote ab)
We won't prove it here, but if you're interested, it all boils down to Pythagoras.
This projection is related to the dot product as follows. By basic geometry, the cosine is the quotient of the length of a by the length of ab. We rewrite this to isolate the length of ab, and then multiply by ||b||/||b||. This shows that the length of ab is equal to cos θ ||a||, which is equal to the dot product aTb divided by ||b||. Since the multiplier 1/||b|| is just a scalar, we can work it into the dot product, making the second argument b/||b||, or the normalized version of b.
That is, when we project a onto b, the length of the resulting vector is the dot product of a with the normalized b.
This doesn't just give us an interpretation of the dot product: by re-arranging the factors, we also get this third way of expressing the dot product, which we’ll call the projection definition.
The dot product between a and b is the length of a projected on to b, multiplied by the length of b.
This leaves us with three definitions of the dot product. We have shown already that the second follows from the first. What about the third? How can we unify the algebraic and the geometric definitions?
The proof is a little involved—and you don't have to know it to do machine learning—but following it is a good exercise in getting comfortable with linear algebra, and many of the notations you need to get used to.
The plan is as follows: We will start with the geometric/projection definition. From that we will show that distributivity holds. This is the hard part: distributivity is much easier to show using the algebraic definition, but we haven't proved yet that they're equivalent.
Then once we have distributivity, we can follow some simple rewriting steps using a set of vectors called the standard basis vectors.
What we want to show is that (b + c)Ta = bTa + cTa. That is, the dot product distributes over the sum.
The first line rewrites the dot product into the projection formulation (which we know follows from the geometric definition).
The second line is the hard part. How do we show that b + c projected on to a has the same length as b projected onto a plus c projected onto a? First, we draw a picture.
Now, imagine rotating this picture (as we’ve done on the right) so that the vector a is aligned with one of the axes, say the 1st axis. In that case, the projection of b on to a is just a vector with element b1 in the first position, and zero’s everywhere else.
Likewise, the projection of c onto a is just a vector with c1 in the first position and zeros elsewhere. And the projection of b + c on to a is a vector with element 1 of b + c, or b1 + c1, and zeros elsewhere This tells us what we want to know: b + c projected on to a has length b1 + c1, and b projected onto a plus c projected onto a also has length b1 + c1.
That is, if the whole picture is rotated so that a points along axis 1, the result follows directly from the way we add vectors. And, since a rotation doesn't change any of the distances in the picture, the same must be true if we don't rotate. This shows that the second line is true.
Now, the third line may look complicated, but remember that ||x|| is just a scalar, so we’re just getting rid of the brackets in a scalar multiplication. The final line follows from recognizing that the two terms are now separate dot products, in the projection formulation, so we can rewrite them in the more familiar dot product notation.
With that, we have shown that distributivity follows from the geometric definition.
Now, we can show that the geometric and algebraic definitions are equivalent. We will assume the geometric definition and derive the algebraic one. The first thing we will need is the standard basis vectors (also known as one-hot vectors). These are vectors that are zero everywhere, except in one place, where they have a 1. We call the standard basis vector that has a 1 in place i the vector ei.
Note that in ei the letter e is bold so this does not refer to the i-th element of a vector but to the i-th vector in some collection of vectors.
With the standard basis vectors we can write any vector as the sum over its elements, each multiplied by the requisite basis vector.
We also know that the dot product of x with basis vector ei is just the i-th element of x. Why? Remember the projection perspective: the dot product of x with ei is the projection of x on to ei, times the length of ei. The projection of x onto axis i is just the i-th element of x and the length of ei is 1.
And with that, we have our ducks in a row. Now, it's just a matter of rewriting.
We start with the dot product (which we take to represent the geometric formulation). In the first line, we rewrite b as a sum over the basis vectors.
In the second line, we used the distributive property, which we showed holds for the geometric definition.
On the third line, we work the scalar bi out of the dot product (this is allowed by the property of homogeneity).
In the third line, we use the fact that a dot product with a standard basis vectors selects an element of the vector (in this case the dot product aTei selects the element ai). This gives us the algebraic definition, which completes our proof.
A matrix is a grid of numbers. Like a vector, it can represent a lot of things, but at heart, that's all it is. When we refer to a matrix, we use a bold, uppercase letter.
This matrix has 3 rows and 2 columns. Whenever we talk about the elements of a matrix, we always take the vertical dimension first and then the horizontal. For instance, we say this is a 3 × 2 matrix (pronounced as "three by two"), and the element at index (2, 1) is 4 while the element at index (1, 2) is 1.
When we want to refer to a specific element of a matrix, we take this index, and put it in the subscript, using the non-bold version of the letter we used to refer to the whole matrix.
Element-wise operations work the same as they do on vectors. If we have two matrices A and B of the same size, we can add them and the result will have at index (i, j) the value Aij + Bij.
An important way to manipulate a matrix is to take its transpose. This simply means interchanging the horizontal and the vertical indices. We indicate this with a superscript T.
You can think of this as flipping the matrix across the diagonal element (2 and 0 in this case). The rows become columns and the columns become rows.
Note however, that the order of the elements in the rows and columns is not changed. In the example above, 4 is the first element in its row before the transposition and its the first element in its column after the transposition.
A particularly common operation on matrices which isn't element-wise is matrix multiplication.
Matrix multiplication takes two matrices A and B—where A has the same number of columns as B has rows—and produces the product C = AB, which has as many rows as A and as many columns as B.
The clearest way to illustrate this is to draw a multiplication diagram like we've done on the left. Note that the horizontal dimension of A needs to match the vertical dimension of B. The other two dimensions can be anything, and these become the height and width of C.
The simplest way to define the contents of C (we've only defined its size so far) is in terms of dot products. Note that for every element of C there is one corresponding row of A and one corresponding column of B (and vice versa). Its content is the dot product of the row of A and the column of B.
Another way to define matrix multiplication is as the sum of outer products. This is less intuitive, but it's sometimes useful in analyses.
The outer product is what happens when we multiply a column vector with a row vector (the opposite of a dot product, which is also called an inner product). The result is a matrix where element i, j is the product of ai and bj.
The relevance to matrix multiplication is that we can also write the matrix multiplication AB as the sum of all outer products of one column of A with the corresponding row of B.
If we denote the k-th column of A as A·k and the k-th row of B as Bk·, then we get the definition on the right for matrix multiplication based on outer products. The lines below that are a short proof that it's equivalent to the dot product definition. Try to follow this proof, it’s good practice in getting comfortable with manipulating matrix indices, which will become important later on.
These are the main rules to remember about matrix multiplication.
Matrix-by-vector multiplication is a specific case of matrix multiplication (if we think of the vector as an n-by-1 matrix). As we see in the multiplication diagram, this yields another vector. If the matrix is square, both vectors have the same dimension. This allows us to think of the matrix as a map: a function that transports every vector in our space to a new position.
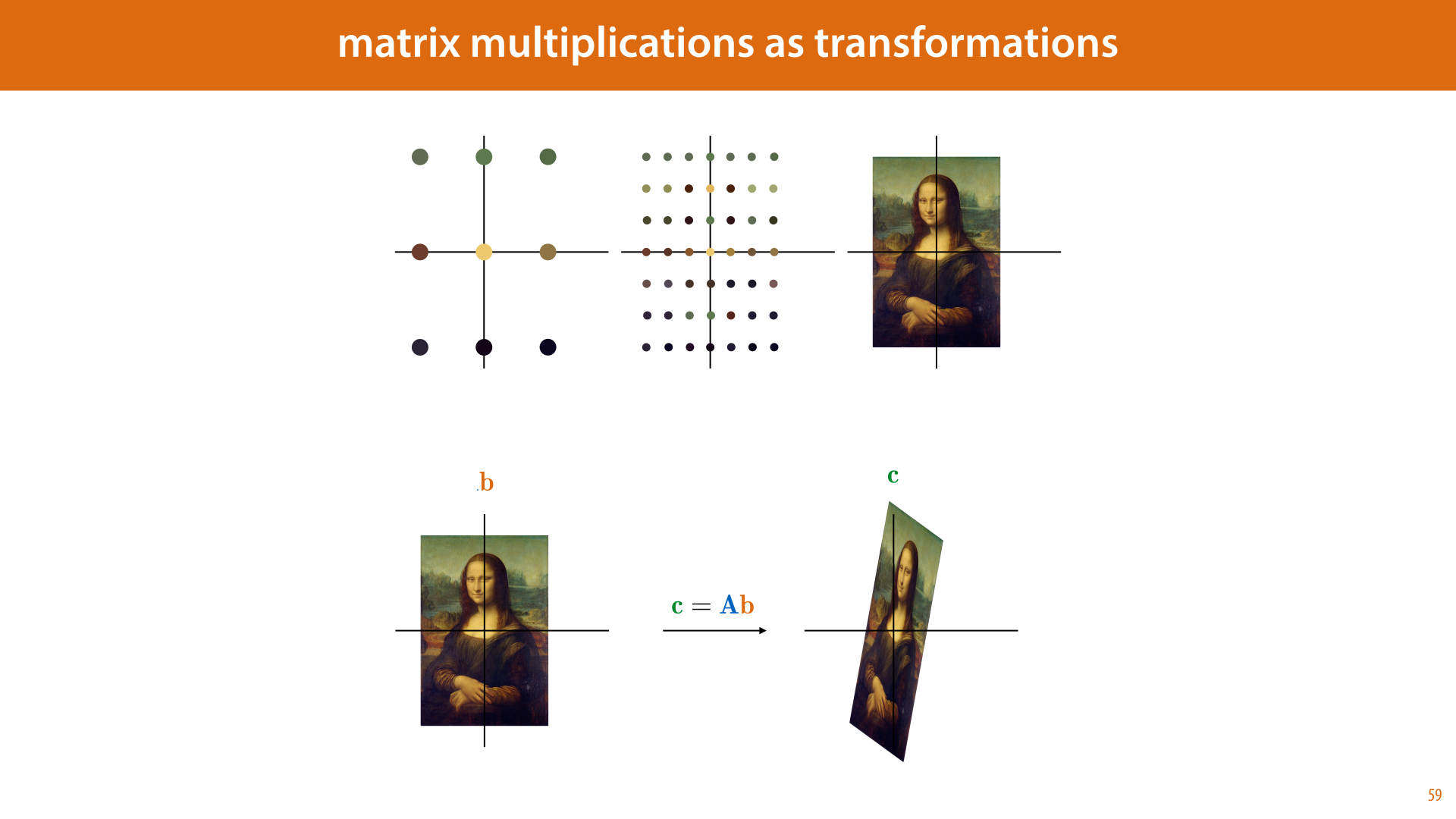
We can think of this as a transformation of our space. Here is a visualization of that in 2D. We start by taking a grid of points, and coloring them according to some image. If the grid is fine enough, it simply looks like we've overlayed the image over the plane.
Then, we multiply every vector b in our grid by the matrix A, resulting in a new vector c. The resulting grid of vectors looks like a squished and stretched version of our original image.
Which transformations can we represent in this way, by a single matrix multiplication? Exactly those transformations that keep the origin where it is, and for which every line before the transformation is still a line after the transformation (or a point). These are the so-called linear transformations.
Some examples of transformations that you can represent by matrix multiplication are scaling, rotation, flipping and skewing, and combinations of these.
If you don't want to keep the origin where it is, you can simply add a translation vector to your function. This turns it from linear to affine (although in machine learning we often use the term linear to apply to both).
We see linear and affine functions a lot in machine learning. This is because they are the easiest to learn. Even the most modern models are based on linear and affine functions, with just enough non-linearity thrown in to make things a little more interesting, but not so much that the function becomes difficult to learn.
These concepts are important to be aware of. We’ll only give you the highlights here. Look them up if you don’t understand what we’re referring to.
The identity matrix is the square matrix that is zero everywhere with 1's along the diagonal. It plays the same role in matrix multiplication as the number 1 does in regular multiplication: multiplying anything by I doesn't change it.
The determinant of a square matrix is a number that expresses how much it shrinks or inflates space (when viewed as a transformation). For instance, in the previous slides, if the picture of the Mona Lisa has twice the area after the transformation as it did before, then the determinant of the transformation matrix is 2.
The trace of a square matrix is the sum of its diagonal elements. It doesn't have a very intuitive meaning, but it comes up occasionally.
The inverse of a square matrix A is a matrix A-1 such that AA-1 = I.
An orthogonal matrix is a matrix for which its inverse is equal to its transpose. This is equivalent to saying that all its columns are unit vectors that are all orthogonal to one another (which implies that this also holds for the rows). As transformations, the orthogonal vectors correspond to the rotations, mirrorings and the identity.
Finally, note that when we distribute the transpose or the inverse over a multiplication of matrices, this is allowed, but the order of the multiplication changes (in the case of the inverse we assume that the inverse is defined for all factors).
In the lectures, we will start writing increasingly complicated equations, using matrices and vectors. Here’s a relatively simple example. If you come up against an equation like this, and you have trouble understanding what it means, or you need to rewrite it in some way, and you don’t know how, there are two time tested techniques to help you figure out what is happening.
The first is to express the equation in a diagram. This will help you visualize the computation. It’s also a particularly good way to check that all the dimensions match. For instance, in this case, we see that this equation only works if C and B are square (that is, they have the same height and width), because the result of ATA will always be square.
The other option is to remember that this is just a concise way of expressing a large number of scalar equations. With a little elbow grease you can always rewrite the equation in purely scalar terms. The safest way to do this is to just put indices on both sides of the equation: both sides represent a matrix, with all elements on the left equal to the corresponding element on the right. This means that the scalar equation top right expresses the same thing.
The right hand side still contains a bunch of matrix operations. We can get rid of this by working the indices inside the brackets step by step. First, the ij-th element of a matrix that is the result of summing two other matrices is just the ij-th element of the first plus the ij-th element of the second. Next, we have the ij-th element of ATA. This is just a matrix multiplication of AT by A. We can fill in the definition of a matrix multiplication from slide 49. Finally, this leaves us with the ik-th element of AT. Since transposing is just interchanging the rows and columns, this is the ki-th element of A.
And with that, we have an entirely scalar equation: Cij = Σk AkiAkj + Bij .
This second trick, rewriting to a scalar equation, is a little involved, but it can be very useful when you have some operation that you want to apply, like taking the derivative, and you know how it works for scalar equations, but not how it works for matrix equations. Then, you can always write the matrix equation as a scalar equation and apply the knowledge you have.
Whenever you get stuck on something involving linear algebra, remember that it's just a concise way of writing down an equation involving lots of variables, which are being multiplied and added. If you don't know how something works in the domain of linear algebra, you can always rewrite it in scalar terms.
It'll be more involved, but it will let you figure out what's happening.
Calculus (short for the calculus of infinitesimals) is the branch of mathematics that deals with differentiation and integration. Fortunately for us, integration rarely comes up in machine learning, so we'll only need to explain differentiation. The flipside of that coin is that we will need to understand differentiation really well.
The reason is that differentiation is an almost magical method for optimization: the business of finding the minimum or maximum of a function. In machine learning we want to fit shapes to data. If we can express as a function how well a shape fits some data, then maximizing that expression will give us an optimal fit. Maybe that all sounds too abstract right now, but that's the big picture: machine learning is basically optimization, and calculus is really helpful for optimization.

There is an old joke that goes something like this. Someone is speeding and is pulled over by the cops. The officer goes "The speed limit is 70 miles an hour, and you were going 90 miles an hour" The driver goes "90 miles an hour? But I've only been driving for 15 minutes."
Ok, so maybe it's not a very good joke. But it highlights an important point about how strange the notion of speed is when you think about it. Let's imagine the cop trying to answer. They might say something like
“Sure, but if you had been going for an hour at this speed, you would have traveled 90 miles.”
The driver would reply: "Not really, because when I started driving I was standing still. And at that off-ramp over there, I would have slowed down. How do you even know what I was doing fifteen minutes ago, you were nowhere near me."
Let's see if we can give the officer a more rigorous answer. It would go something like this.
“Sure. But what I did to establish your speed was to measure how far you traveled over a small interval of time, say one second. Over such a small interval you can't meaningfully change your speed, so we can treat it as constant. We then extrapolate: how far would you travel if you kept going like that for an hour: if you had traveled the same distance you traveled in that second for the remaining 3599 seconds. This is what we call your speed in miles-per-hour.”
It's a bit of a mouthful, and it may be hard for the police officer to maintain their natural authority through an answer like this. But it shows us that something quite subtle is happening when we talk about speed.
Here's a little diagram to help us understand. We'll assume that the driver drove away from home in a straight line, so we can measure their position as a single number on the vertical axis.
We see here that at no point did the driver have a constant speed. That is, at no interval, no matter how small, did they cover the same distance in the first half of the interval as the second. What we can say, however, is that as the interval gets smaller, the difference becomes smaller as well. That is, the more we zoom in, the more the curve looks like a straight line.
Like our cop in the previous example, we can take the linear way that the function behaves in this tiny interval, and extend it: we imagine that the driver drove the way they did in the interval for a longer amount of time: at a constant speed. The further we get from our interval, the less this looks like what actually happened, but near our interval, it's a pretty good approximation.
To make this more precise, we start with an interval defined by two points. We draw a line through the two values of our function at that point. As the points get closer to each other (the interval gets smaller), this line becomes a better and better approximation to our curve, within the interval.
In the limit, as the points gets closer and closer together, we get a line that just touches the curve at a single point. This is called a tangent line.
We want to specify what this tangent line actually looks like. The specific property of the tangent that we're interested in is the slope. How much it rises if we take a step of size 1 to the right.
Let's say our leftmost point is x and the other point is a distance of h to the right of it, at x + h. We mark two points on the curve of f at these points and draw a line through them. What is the slope of this line, and what happens to that slope as we make h smaller and smaller?
Over the space from x to x+h this line rises from f(x) to f(x+h). That is, over a horizontal interval of size h, the line rises by f(x + h) - f(x). If we want to know the vertical change for one unit of horizontal change (one step to the right), we divide f(x+h) - f(x) by h. This is the slope of the orange line. The horizontal distance, the size of our interval, we'll call h. In this case h is bigger than 1, but the formula works the same for h smaller than 1. The question is, what slope do we converge to if h gets smaller and smaller?
The problem is that once the two points come together, with h=0, there is no longer a single unique line through it/them. This shows in the formula by the fact that we get a division by zero. The whole thing becomes undefined.
We need to figure out what the tangent converges to. We make the distance between the two points smaller and smaller, without letting it get to zero, and we look at the behavior of the line through them. This line will eventually get closer and closer to one specific line, as the two points get closer and closer to each other. This is how we define the tangent line.
The slope of the tangent is called the derivative. It is the slope of the line we get in the limit if we shrink the distance between x and x' to be smaller and smaller.
What the slope of the tangent is, depends on where we are on our function, just like our driver's speed was different at every point in time, we get a different value for the derivative at every point on a curve.
Just like we can plot a driver's speed over time, we can plot the slope of the tangent of f(x) for every x. This gives us a second function of x, which is often labeled f'(x) and called the derivative. Working out what a derivative looks like is called differentiation (or "taking the derivative") .
We can work out some basic rules about what to expect from the derivative, based on what we know:
If the function f(x) increases at x, then its derivative should be positive at x, f'(x) > 0. This is because the slope measures how much the tangent increases if we take one step to the right. If it does increase, this is a positive number.
Likewise, if f(x) decreases at x, then its derivative should be negative at f'(x).
Finally, if f(x) neither increases, nor decreases, that is when f(x) is the tip of a peak, the bottom of a valley, or simply a flat region, then the derivative should be exactly zero.
Here's how all of that translates to a mathematical definition. We take the definition of the slope over an interval (x, x+h) that we saw earlier, and we see what that slope converges to as we make the interval smaller and smaller.
This is what the "lim" operator does: it says take the process at the bottom (h -> 0) and finds out what the thing on the right converges to under this process. In this case, we can't set h = 0, because we would get a division by zero, but we can let h go to 0.
One of the great achievements of calculus is that if we happen to have a functional form for f(x), that is we can express it in a formula like f(x) = x2 + x +1, then we can also work out the functional form of the derivative f'(x). This is called taking a derivative.
The way we do this is by starting with this definition and applying some simple rules that we know always work for limits. This has led to a set of general rules for taking derivatives, which we can use to get from almost any function f(x) to its derivative f'(x).
To work out the following examples, we'll need to know how to think about limits. In a proper calculus course, we'd take you through both the intuition behind them and then derive the rules for correctly working out algebraic derivations with them.
However, once we've used limits to derive the rules for differentiation, we won't see them again in the rest of the course, so we can allow ourselves a little shortcut. There are only three things we need to understand about how limits work.
First, the function for which we take the limit, g(x) here, can be rewritten using any of the rules of algebra. This just turns it into the same function, expressed differently, so it doesn't change the limit we're expressing with the notation "lim g(x)".
If the function to the right of the "lim" is a sum of two other functions, like x2 + x is a sum of the functions x2 and x, then the limit of that sum is just the limit of the first term by itself plus the limit of the second term by itself.
If our limit is for h going to zero, and the function to the right of "lim" is just h by itself, then the result is just 0. This hopefully makes intuitive sense: if we make h smaller and smaller so that it converges to zero, then the function "h" becomes zero.
If the function c to the right of "lim" is constant with respect to h. That is, it cany be any expression, with any number of variables, but it doesn't contain h, then the result is just c. Again, this should make intuitive sense. If we make h smaller and smaller, but its value doesn't affect c, then the result will just be c.
To properly work out all limits you might encounter, you'll need a little more than this (not much though), but to illustrate the principle we can make do with these four rules.
Here is an example for the simple function f(x) = x2.
First, we write down what it is we're interested in: f'(x). The only thin we know so far is the definition of the derivative, so we fill that in.
Next, we notice that f(x+h) and f(x) appear. These we can replace using the definition of f(x). This is just rewriting the function to the right of the "lim" into something equivalent. That means that the limit we had before we rewrote it is the same as the limit afterwards.
Next up, we can rewrite the term (x + h)2 into x2 + 2xh + h2.
The first and last term are x2 and -x2, so these cancel each other out. Next up, we are dividing by h, so we remove one factor of h from each of the terms above the division line.
Finally, we are left with the limit of 2x + h as h goes to zero. This limit we can solve by the rule from the previous slide, and setting h=0.
Here is another example. This shows a powerful principle: we can often work out basic rules, by not specifying what all the details of a function are. In this case, we don't specify what f(x) is, we just say that it is the sum of a function g(x) and another function k(x). Anything we can work out about what f'(x) looks like without specifying the details of g(x) and k(x), must then hold for all functions that look like this.
We start by filling in the definition of the derivative, and filling in the definition of f(x) (lines 1 and 2).
We then group the terms for g and the terms for k together, and split the division into two divisions (lines 3 and 4).
We can now apply the sum-rule for limits, and split the limit into the sum of the limit for g and the limit for k. (line 5)
Finally, and this is the magic trick, we recognize that these two terms both correspond to the definition of a derivative. We can do the opposite of "filling in the definition" that we did in the first line. We replace the definition of g'(x) with the label g'(x) and likewise for k'(x)
The end result is the sum rule. It states that if our function is the sum of two others functions, then its derivative is the sum of their derivatives.
That hopefully gives you some intuition for where the rules come from. The rest of the rules we will just give you to memorize.
Pay particular attention to the second exponent rule. It tells us that the derivative of the exponential function bx is proportional to itself. That is, it's just the same function again, but multiplied by some constant independent of x (a constant that happens to be ln b). This suggests that if there is some value of b for which this constant is equal to 1, we get a function that is equal to its own derivative. It turns out that this happens is b = 2.7182818284... This number we call "e", Euler's number. The logarithm with base e, we call the natural logarithm (we already saw this in the first part of the lecture).
The other rule that you should pay attention to is the chain rule. It is no exaggeration to say that the method that drives 90% of modern machine learning is derived from this one simple rule. It's hard to convey exactly why just yet, except to say that when we design complex models, we do it by chaining functions together: making the output of one the input of the next (much like we build computer programs). The chain rule gives us a derivative over such chains of functions.
The notation on the left, using f' to indicate the derivative of f, is probably the most precise notation, and the best suited for explaining the principles of calculus in general.
However, in machine learning, the notation we use almost exclusively is the one on the right: Leibniz's notation. It can be a little bit more work to get used to this way of writing derivatives. All I can say at this point, is that it pays off eventually. For now, let's take a closer look at where this notation comes from and at how exactly it's defined.

Leibniz is one of the two inventors of calculus, the other being Newton. Neither of them were particularly obsessed with mathematical rigour. They worked things out based on intuition and guesswork, being as much physicists as mathematicians. They were looking for the fundamental rules that governed the world, and a lucky guess followed by an experimental verification on a few examples was perfectly acceptable.
The way both of them though about calculus was in terms of infinitesimal quantities. Numbers that are as close to zero as you can possibly get, but not equal to zero: something infinitely small but bigger than zero.
It was in terms to these infinitesimals that Leibniz developed his calculus. For a function f(x), an infinitesimal change to x, which he called dx, would cause an infinitesimal change to f(x). The latter would also be infinitely small, but still potentially different from dx.
If you think this all sounds a bit fuzzy and imprecise, modern mathematics agrees with you, but the key property that Leibniz cared about was that the quotient between the two quantities (one divided by the other) could be worked out.
And in this respect, Leibniz wasn't wrong. This is still the idea behind the derivative: we make a small change to x and see how much f(x) changes as a result. Then we divide the latter by the former. If the result converges to some fixed value as the small change goes to zero, we have a well-defined derivative.
It's just that the language of limits had not been established yet, so Leibniz couldn't write his ideas down with the rigour we have available today.
For this reason the Leibniz notation is usually re-interpreted from how it was originally intended. It looks like we’re dividing one quantity by another, but that's not what it represents.
The d·/d· notation actually represents an operator, it takes a function as its argument, written to the right or above the line, and returns another function: the derivative of the argument. The letter below the line (x) represents the variable that we take the derivative for.
The main benefit of the Leibniz notation is that you don't have to refer to your function by an explicit name like "f(x)". You can just fill in its formula directly into the operator. Here we say that for f(x) = x2 the derivative is f'(x) = 2x in one single statement. This is one reason we prefer the Leibniz notation in machine learning: it makes long derivations simpler to write down.
Here are two forms of shorthand we will occasionally allow ourselves, to simplify the notation. At the top, if it is clear that the result of f is a function of x, we will omit its argument. You can think of this in Leibniz's terms if you like: we divide the change in f by the change in x. What is left more implicit by this notation is that we create the change in x, and observe the resulting change in f.
The second line shows what happens when we fill in the explicit functional form of f in terms of x. We will do this very often. Technically, we need to put brackets around the whole function, or the statement might be ambiguous (especially if we write the function to the right of the division line as in the previous slide). In practice, things look a lot clearer without the brackets, so if the potential ambiguity is minimal, or can easily be resolved from context, we allow ourselves to leave the brackets out.
Here are some examples. The first two lines show the derivatives we've already worked out in the Lagrange notation.
The right part of the second line shows how much clearer things can become when we assume that we know which variable is dependent on which. The notation is more ambiguous, but a lot clearer.
The third line shows the benefit of indicating the independent variable. The variables a, b, c are indicated with letters in the function, but we treat them as constants: x is the only variable we change to observe the resulting change in the function above the line. The rest is treated the same way as the 3 in the exponent is.
Here are the basic rules again, but this time in Leibniz notation.
Pay particular attention to what we're doing for the chain rule. In the first factor on the right hand side, we are taking the derivative with respect to a function of x, not x itself. This can be a little tricky to wrap your head around, but it's a very powerful way of writing derivatives.
Let's look at a simple example of the chain rule in Leibniz notation.
The function (x-3)2. We can see this as the function x-3 fed to the function that squares its input.
Applying the chain rule means first taking the derivative of this “squaring function” with respect to its input. The input to the squaring function here is not x, it's (x-3). So we want to take the derivative of (x-3)2, but treat the whole expression x-3 as the input. This is what the factor in blue represents: we are taking the derivative with respect to (x-3). When we look at it like that, the exponent rule applies, and the result is simply 2(x-3).
We then multiply this derivative with the derivative of x-3 over x, which is 1.
We will use the chain rule a lot, and always write it like this. Make sure you understand what is happening in this slide.
The final subject we will need to discuss is multivariate or multivariable calculus.
This is the kind of calculus you use when your function has multiple inputs and/or multiple outputs. Luckily, the basic principle is almost the same as for functions of one variable.
We will see a lot of functions with multiple outputs, but we will never apply calculus to them. We will only ever take derivatives of functions with a single output. Happily, this simplifies things a little bit.
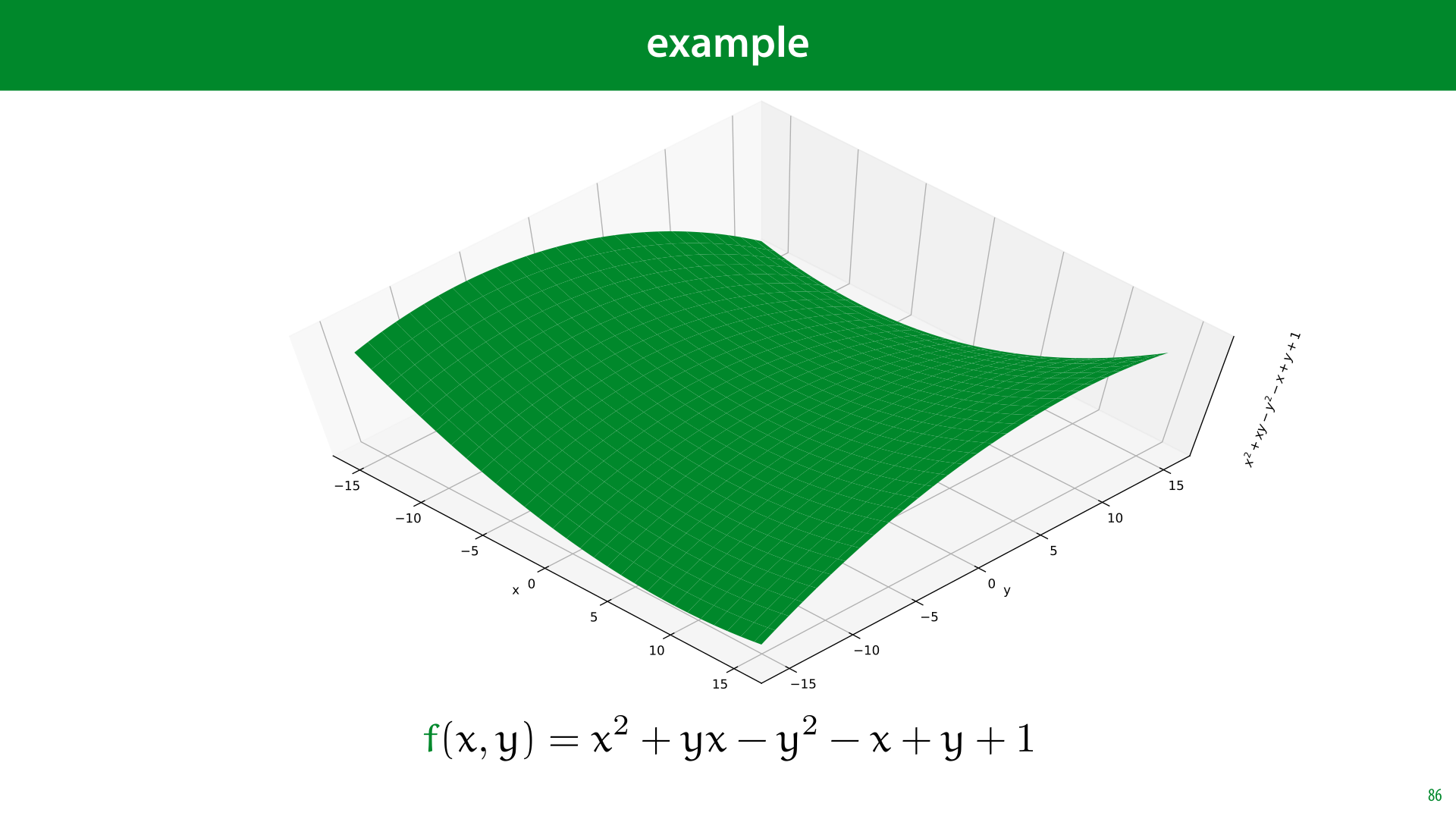
The simplest example is a function with two inputs and one output. Here's some arbitrary polynomial in arguments x and y,
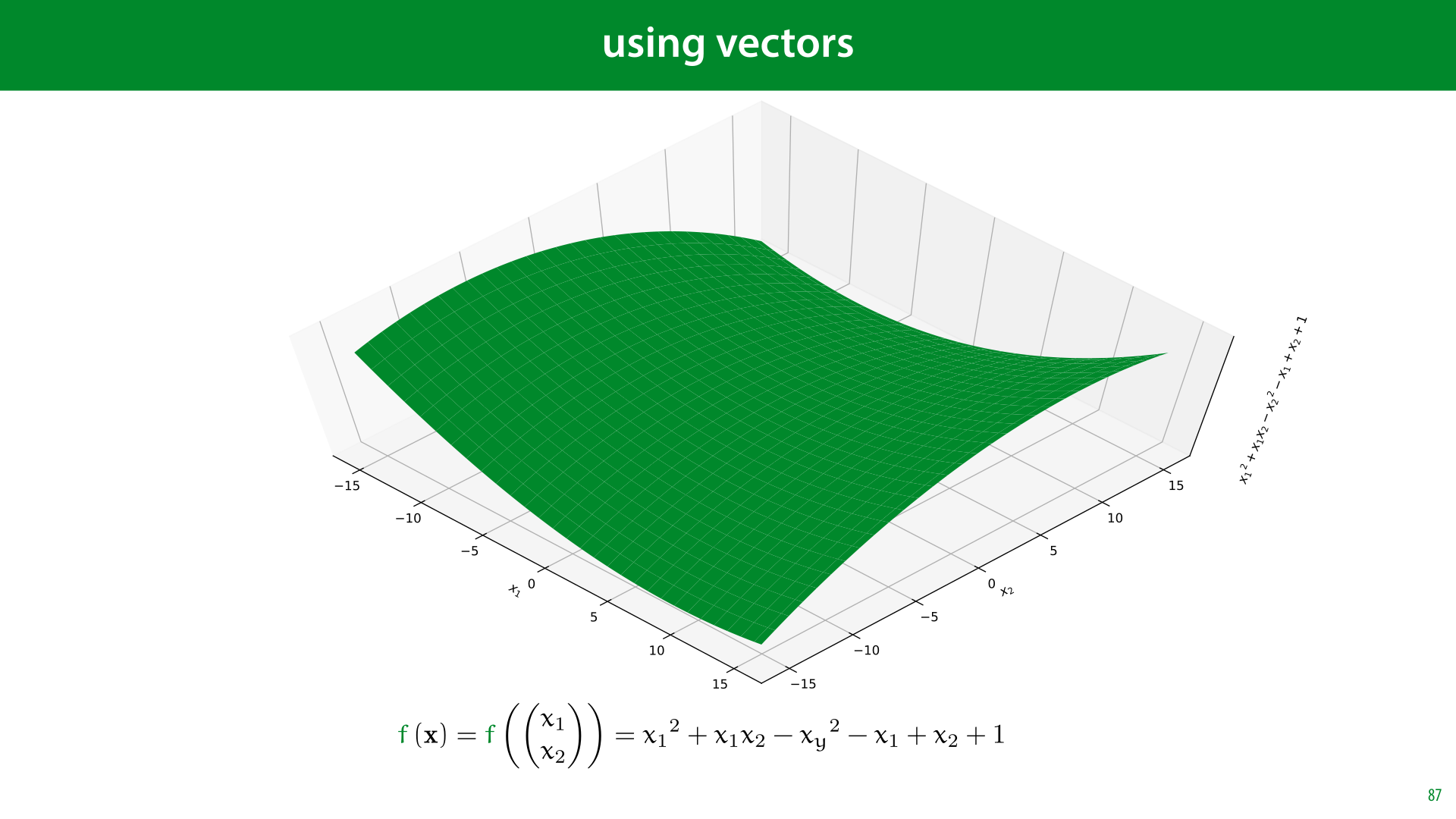
We can use vectors to easily express a function of multiple variables. Here is the same function as before, but now expressed using a single vector argument.
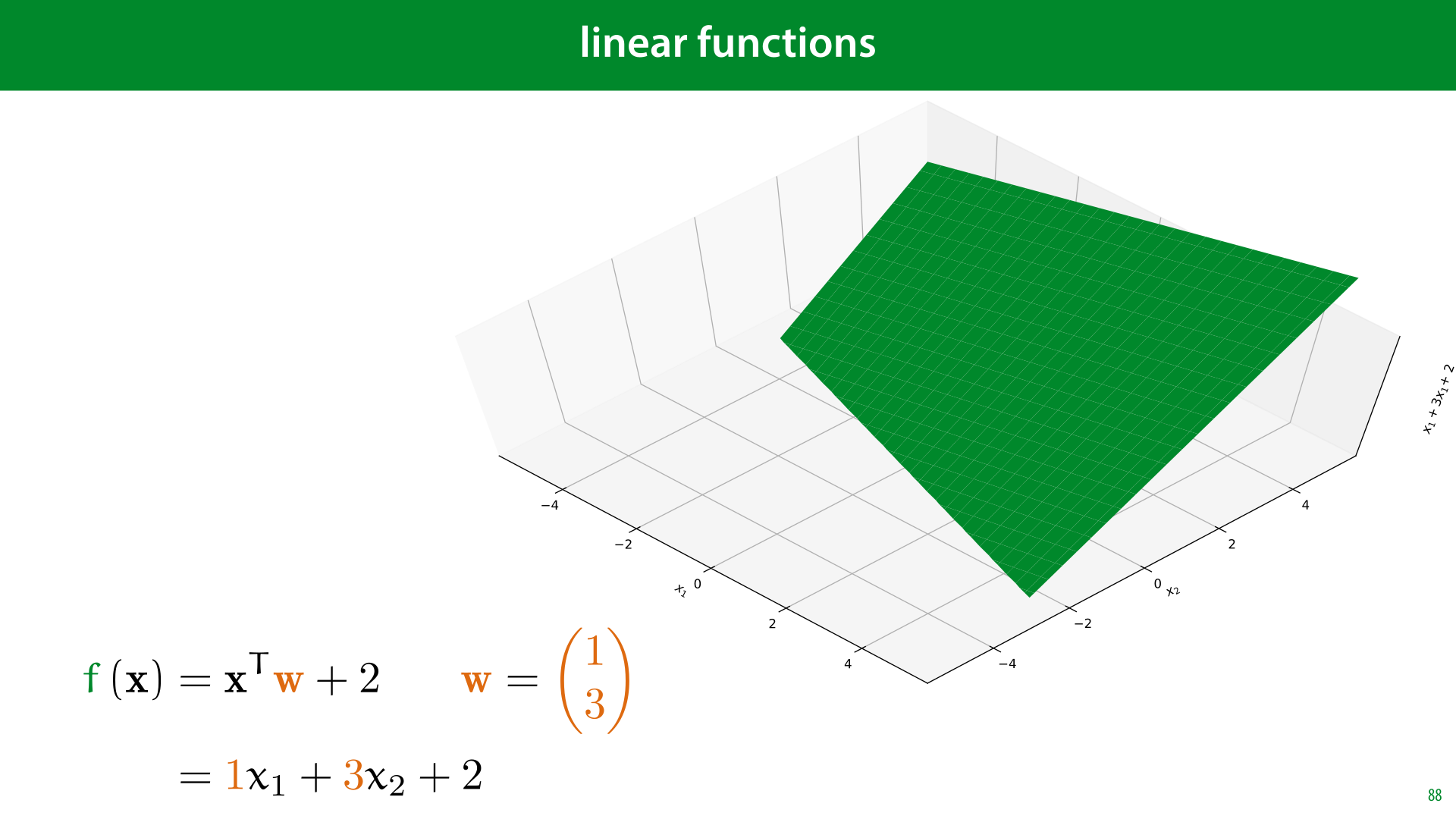
One particularly simple type of vector function, which we will see a lot is a linear function. In this function, we take the dot product of the input vector with some other constant vector (and possibly add a constant scalar). Such a function draws a flat plane.
If the function has more than 2 arguments, we call the resulting structure a hyperplane.
Here's how to interpret the parameters of a linear function. Note that in a 1D linear function, f(x) = wx + b, the constant w is the slope, how much the function moves up if you take one step to the right, in a 2D function the values w1 and w2 provide two slopes. How much the plane moves up if you take a step of 1 along the x1 axis and how much the plane moves up if you take a step of 1 along the x2 axis.
The term b doesn't change the angle of the plane, but serves to translate it up and down.
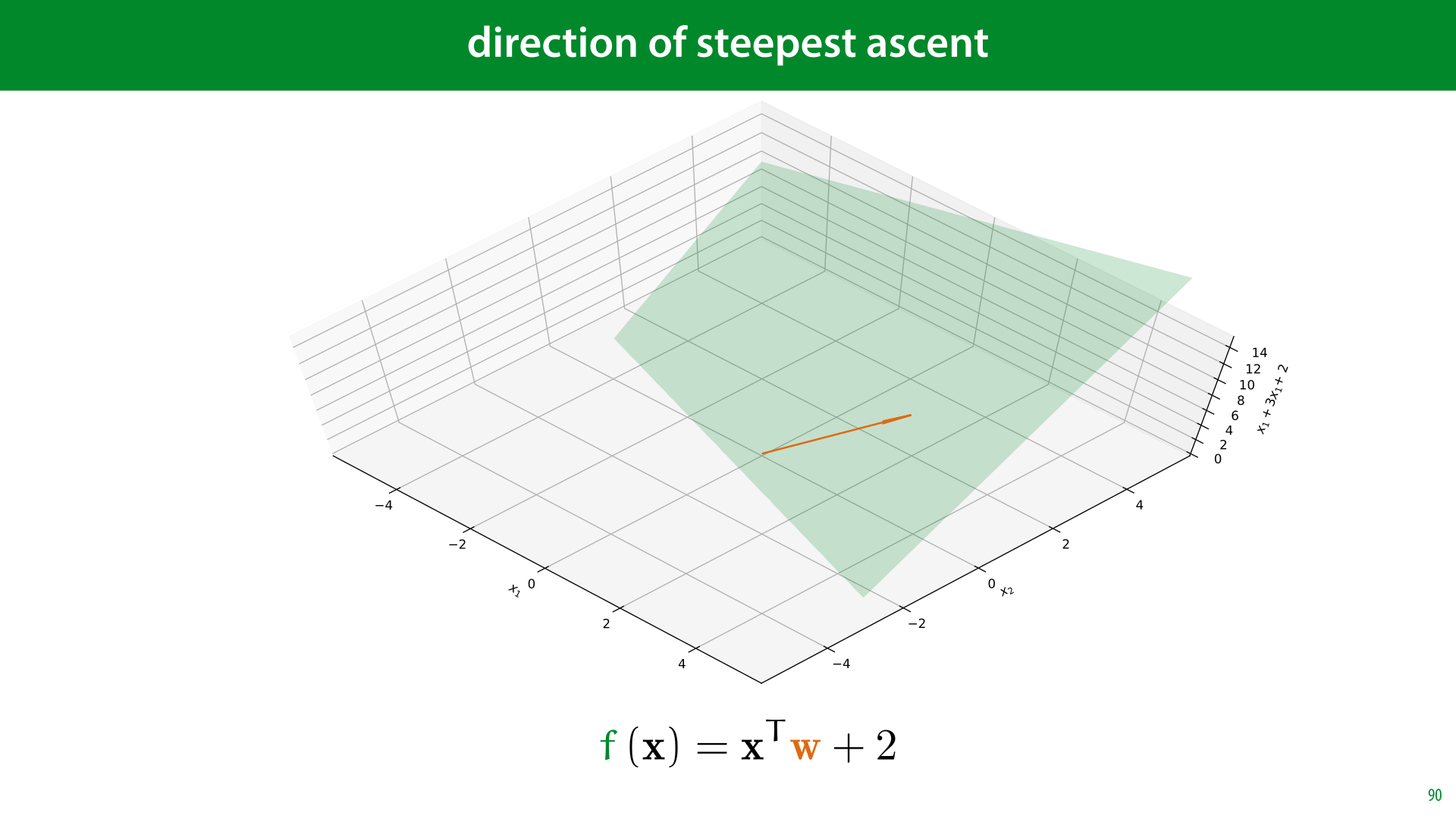
One fact that will become very important is the meaning of the vector w in linear functions like these. It has a simple interpretation. When we view it as an arrow in the x1/x2 plane, it's the direction in which the (hyper)plane of our function increases the quickest. Wherever you are, if you want f(x) to increase as much as possible, move in the direction of w.
To prove this, we can first make a few simplfying assumptions. The question is, in which direction does f(x) = xTw + b increase the quickest. The scalar b only translates the hyperplane up and down, it doesn't change its angle. Therefore, the answer is the same for f(x) = xTw + b as for f(x) = xTw.
To make our question more precise, we need to state what we mean by a direction. We can represent this by a unit vector u (a vector with length 1). The question is then for which unit vector u is f(x + u) the largest.
Finally, note that in a hyperplane, it doesn't matter where we start. The direction of greatest ascent is the same at all points. So we can set x=0. The question then becomes for which unit vector u is the value f(u) = uTw the greatest?
The question is easily answered by switching to the geometric definition of the dot product. The question then becomes, for which unit vector u is f(u) = ||u|| ||w|| cos θ the greatest. Since u is a unit vector, this becomes f(u) = ||w|| cos θ. The only part of this expression that the choice of u affects is θ, the angle between u and w. We maximize cos θ by making the angle minimal, which means that we maximize f(u) if u points in the same direction as w, which completes our proof.
Now, let's look at what a derivative means in the context of a multivariate function. The first thing we define is a partial derivative.
This is simply the derivative as we already know it, with respect to one of the arguments of the function, treating the other as a constant. For a function f(x, y) with two arguments, we can take two partial derivatives. One with respect to x and one with respect to y.
When we take a partial derivative, we replace the d from the Leibniz notation with the symbol ∂. This has the exact same meaning, it only signifies that the function you are taking derivatives over has more than one symbol, and that you are treating the others as constants. Since almost all functions in our course are multivariate, we will always use the ∂ symbol from now on.
Here is an example (the function for which we plotted the surface earlier).
When we take the partial derivative with respect to x, we treat all the ys as constants. This means that when we get to the term xy, The result is y times the derivative of x over x, which is 1, so the derivative for that term is y.
When we then take the derivative with respect to y, the opposite happens, and the derivative is x.
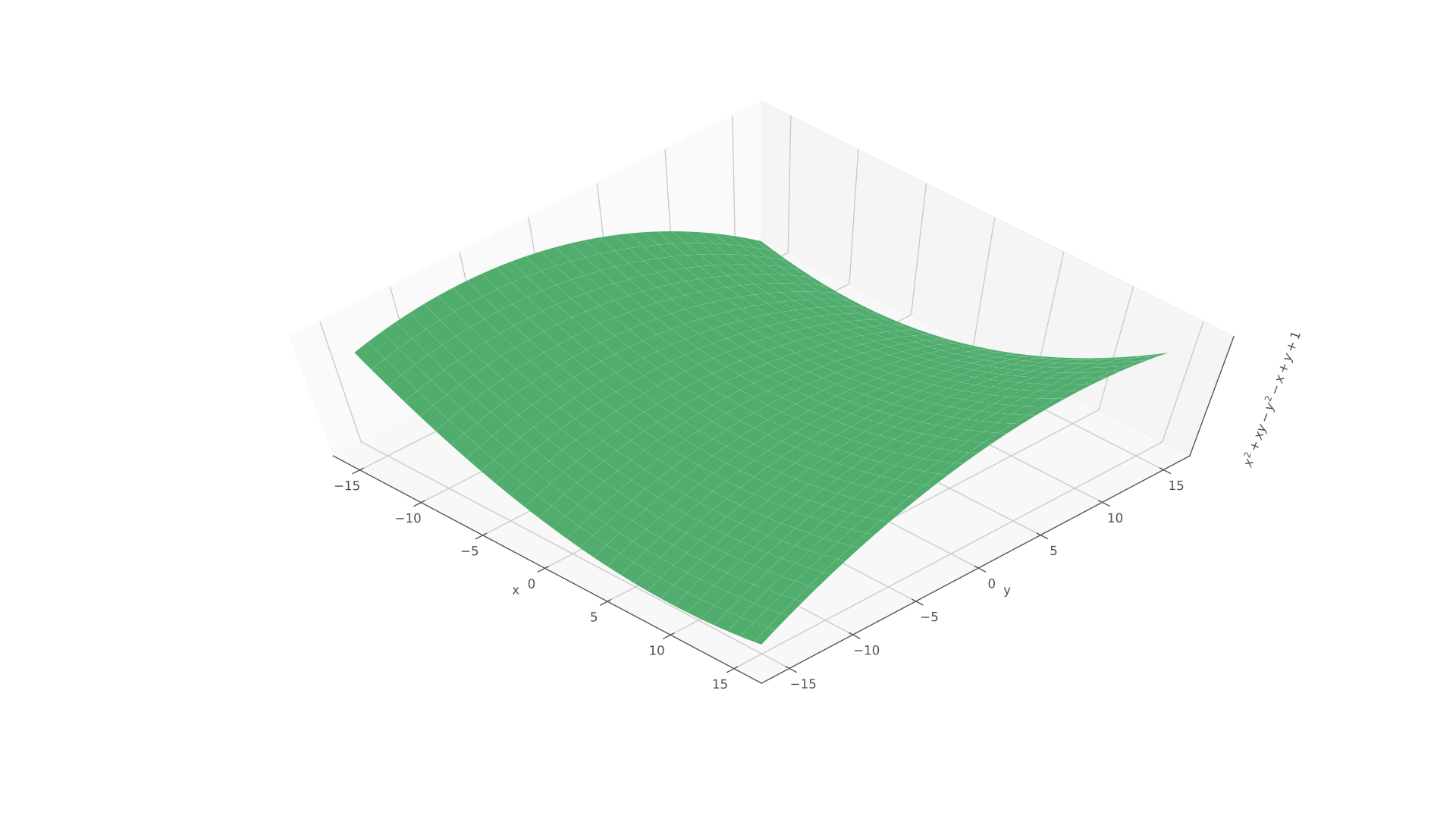
Here's a visualization of what it means to take the partial derivative as a point x=0, y=5, with respect to x.
We let the function vary with x, keeping y fixed. This gives us a kind of "slice" through the surface f. The result is that we have a one-dimensional function again, for which we can take the derivative. We do this by only caring about the way f changes if we change x. In other words, by treating y as a constant.
Then we do the same for y, treating x as a constant.
For both curves, the derivatives give us the slope of the tangent line. We've shown these as dotted lines here.
These lines cross the same point, so together, they lie in a shared plane. In higeher dimensions, the tangent lines of all partial derivatives lie in a shared hyperplane. This is the tangent hyperplane. The hyperplane that just touches the surface of f.
How do we describe the tangent hyperplane? Note what the tangent slopes indicate: how much the plane moves up if we take a step of 1 along the x axis and how much the plane moves up if we take a step along the y axis. These are exactly the roles of the constants in the function xw1 + yw2 + b. Or, in vector notation the elements of the vector w in the function xTw + b.
This tells us that if we take all of our partial derivatives and stick them in a vector w, the function that will describe our tangent hyperplane is xTw + b (for some value of b, which we don't usually care about).
Here is the whole process again in a simple animation.
We start with a function with two inputs and one output. In this case the function f(x, y) = x2 + y2 - ¼xy + x - y +1
We pick a point on the function, in this case (10, 20).
We can define two partial derivatives. One is the derivative of f as x varies and y is kept fixed.
The other is the derivative of f as y varies and x is kept fixed.
Both of these are functions of one variable, so we can apply what we know from univariate calculus to work out the derivatives. At our point (10, 20), this gives us a tangent line touching the red function and a tangent line touching the blue function.
Since these lines cross, they lie in a shared hyperplane. That is the plane that (in most cases) just touches but does not cross f. Like the tangent line, the tangent hyperplane functions as a locally linear approximation of f: in a small enighborhood around the point (10, 20), it behaves as much like f as any linear function can.
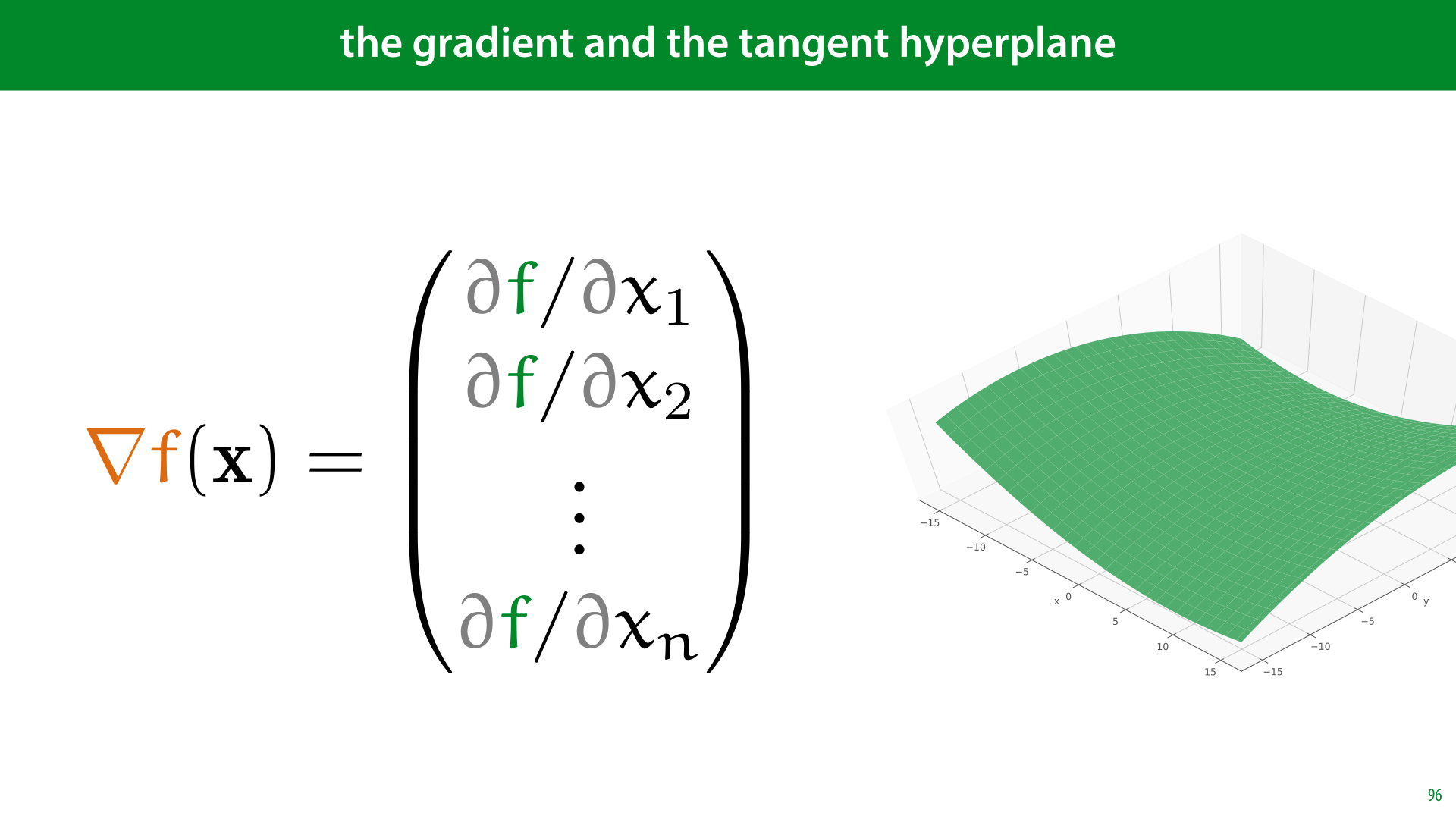
This vector, containing all partial derivatives, is called the gradient.
The gradient is the "slope vector" in the function describing the tangent hyperplane.

On the left is a screenshot of one of the most popular online magazines about machine learning. It's called The Gradient. This should tell you that the gradient is a very central idea in machine learning.
The reason is the same as before. In machine learning, the main thing we care about is optimization, finding the highest or the lowest point of a complicated function: solving an argmin problem.
The tangent hyperplane is a local approximation of a function. In general it behaves nothing like the function, but in a very small neighborhood where the two just touch, the tangent hyperplane is a great approximation. That means that so long as we stay in that neighborhood, we know where to move it we want the function to increase.
The idea is that we take a small step in that direction, and then recompute the gradient. This gives us a new, slightly different direction to move in, which allows us to take another small step and so on. So long as we take only small steps before recomputing the gradient, we will always be following our function. This is called gradient ascent. If we want to find the minimum of a function, we take the small steps in the opposite direction
Probability is an important tool in Machine Learning. We expect that you have been taught probability theory already, but since it’s a subtle concept, with complicated foundations, we’ll go over the basics again in this first video.
If you have never done any probability before, please consult the homework exercises and the recommended reading to brush up first.
To start, let’s look at the way we use probability informally.
Let’s say you are a concerned parent, you read this headline and you are shocked by it. You turn to your partner, and you say “that means that the probability that our son is gambling online is 12.5%”. Your partner disagrees, you have a good handle on your son’s behaviour and his spending. Unless he has a credit card you don’t know about, and the probability of that is much lower.
Well, then the probability that Josh, his closest friend, gambles online must be 12.5%. If one in eight teenage boys is gambling, they must be hiding somewhere. Your partner disagrees again: probability doesn’t enter in to it. Josh is either gambling or he isn’t.
Clearly, we need to look at what we mean when we say that a probability of something is such-and-so. There are two commonly accepted ways of looking at it: objective and subjective probability. We’ll start with objective probability.
image source: https://www.theguardian.com/society/2016/sep/20/one-in-eight-european-teenage-boys-gamble-online-says-survey
In objective probability, “the probability that X is the case” represents an objective truth: whatever a probability is, it must be the same for everybody. You and I may disagree over a probability, but only because one of us is wrong. There is one true probability. An example is the probability that a coin-toss will land heads. If nothing unusual is going on, everybody should agree that the outcome is uncertain and that the probability will be 50%. We can't have a situation where one person thinks it's 10% and the other thinks it's 90% and they're both right.
The most common form of objective probability is frequentism. Under the frequentist definition, probability is a property of a (hypothetical) repeated experiment. For instance, take the statement “the probability of rolling 6 with a fair die, is one in six.”
The experiment is rolling a die. The outcome we are discussing is the roll resulting in a 6. If we were to repeat the experiment a large number of times, N, then the proportion of times we observe the discussed outcome is close to 1 in 6. More precisely, as N grows, the proportion converges to 1 in 6.
Under a frequentist interpretation, saying “the probability is one in six", is equivalent to saying “if I roll the die repeatedly, the relative frequency of sixes will converge to 1 in 6 as the number of rolls grows.”
Under objective probability the statement “the probability that Josh is gambling is 12.5%” is indeed nonsense. There is no experiment we can imagine where Josh “turns out" to be a gambler one in 8 times. He either gambles or he doesn’t.
What we can say is that the probability that a teenage boy drawn randomly from the European population gambles online is 12.5%. This is an experiment we can repeat, and at every repetition, we choose a different boy, so we get a different outcome.
The alternative to objectivism is subjectivism. It states that probability expresses our uncertainty. If X is a boolean variable, one that is true or not true, and we are uncertain whether X is true, we can assign a probability to X being true. A probability of 0.5 means we are entirely ambivalent, a probability of 0.75 means we think X is pretty likely, and a probability of 1 means we’re entirely sure that X is true.
In this case, different people can have different probabilities for the same thing being true. You and I may "assign" different probabilities to something being true and both be right. If you have information I don’t have, your probability may be closer to certainty than mine.
Bayesianism is the main form of subjective probability. It builds on Bayes’ rule, which we will discuss later, to tell us how we should use observations to update our beliefs.
Under subjectivism, we can say “the probability that our son is gambling is 12.5%” We don’t know precisely what he gets up to, so even though there is a definite objective answer, we are uncertain. If we know only this headline, we may well pick 12.5% as our belief that our son is gambling. Of course, as noted before we have a lot more knowledge about our son than about other teenage boys. We know he goes to bed on time, we know where he gets his money, and we know he probably doesn’t have a secret credit card. So even though the probability for a random teenage boy would be 12.5%, the probability for our son is actually much lower, because we have extra information.
This is the fundamental difference between the two views: under frequentism, probability is defined as an objective property of the world. The probability of X is the same for all people regardless of what we know or don’t know. Under Bayesianism, probability is an expression of a subjective property: it can change from one person to the next, and if we learn new information, it can change from one moment to the next. If we find out that our son does have a secret credit card, the probability that he is gambler, suddenly jumps up dramatically, even though nothing about him has changed, only our knowledge about him.
Note that Bayesianism, in a sense encompasses frequentism. If we define probability as the outcome of a repeated experiment, then before we do the experiment we are uncertain about its outcome. If we understand the experiment perfectly, then the Bayesian probability we assign to the outcomes will coincide with the frequentist probabilities of the outcomes.
So, at heart subjectivism and objectivism are disambiguations. The word probability is ambiguous, and these additional terms allow you to be precise in what you mean.
Note that you don’t have to commit to one view or another. Subjective and objective probability are just ways to be more precise about what the word probability means. You can use the subjective definition one day and the objective definition the next.
However, once you start doing statistics, the two definitions lead to fundamentally different approaches (which we’ll see in more detail later). And in the statistical community there are definitely two camps: the frequentists and the Bayesians, and arguments between the two can get very heated.
Since machine learning is often seen as another form of statistics, you may ask whether it is usually seen as using subjective or objective probability. I can’t give you a commonly accepted answer, I think opinions differ.
All that was about the interpretation of probabilities. This is what the field of statistics is about. We have frequentist statistics and Bayesian statistics.
The mathematical definition of probability, studied in the field of probability theory, which is very different from statistics, is entirely distinct from the question of how probability applies to the real world. Both frequentists and Bayesians use the same mathematical framework to express probability as a number between 0 and 1. The only difference between them is in what this number is taken to represent.
We’ll go through the basic ingredients of probability theory quickly. This is a complex field, and a complete basis is too technical for this course. We'll handwave some of the technical details, and you can hopefully get by with a little bit of intuition.

First the sample space. These are the single outcomes or truths that we wish to model. If we flip a coin, our sample space is the set of the two outcomes heads and tails.
We can have discrete sample spaces or continuous ones. In a continuous space, you can imagine that in between any two values there is always another value (like when we measure someone's height very precisely). In a discrete sample space this isn't usually the case.*
A discrete sample space can also be infinite: consider flipping a coin and counting how many flips it takes to see tails. In this case any number of flips is possible, so the sample space is the natural numbers (although any number larger than 40 will get an astronomically small probability).
From the sample space, we construct the event space. Events are those things that can have probabilities. These include the elements of the sample space, like the probability of rolling a six with a die, but they also include sets of multiple elements of the sample space, like the event of "rolling a one or a six" and the event of "rolling an even number". Even the empty set and the set of all six numbers are events. As we will see, these will get probabilities 0 and 1 respectively.
The events containing only one element of the sample space, like "rolling a 1", are called atomic events.
How the event space is constructed is a technical business. For our purposes, we can simply say that if the sample space is discrete, then the event space is the powerset of the sample space: the set of all possible subsets we can make.
For continuous sample spaces, not every subset can be an event. We need to make sure that our event space is a thing called a “sigma algebra.” We won’t need to worry about this in this course. We can simply trust that if we don't try to assign probability to any particularly unusual subsets of the sample space, everything will work: these will be in the sigma algebra, so they will be events, and we can assign a probability to them.
Random variables help us to describe events. We can think of a random variable D as something that takes the values in the sample space, so that we can use it to describe events: instead of describing an event like "rolling a number larger than three" in natural language, we can describe it symbolically using the random variable D as "D > 3". This usually makes our notation more concise and precise.
We usually use capital, non-bold letters for random variables, or a capitalized word, and lowercase letters for traditional variables. A statement like "D=d" refers to the event that the random variable takes the value that the regular variable d currently represents.
Once we have a way to describe the events we are interested in, we can assign a probability to each event. We do this with a probability function p. This function must satisfy several constraints, but we’ll take those as read for now, and just say that it takes an event, and maps it to a value between 0 and 1 (inclusive).
In probabilistic machine learning, it’s common to model features, target labels, and sometimes even model parameters as random variables. If we are referring to a dataset of multiple instances, we model each as a separate random variable with the same distribution. We'll see some examples later in this lecture.
Interpreting what a statement including a probability function means depends on whether all variables are “filled in.”
In the first line, X=0 refers to a single, well-defined event, so p(X=0) refers to a single value between 0 and 1. In the second line we have a regular variable x, so the statement “X=x” can refer to different events, depending on what x is. In other words, here “p(X=x)” is a function of x. For example, if x can take one of two values, -1 or 1, then the function p(X=x) has a range of only two values as shown here.
Since we usually know which outcomes belong to which random variables, p(X) and p(x) can both be used as shorthand for p(X=x).
If we have a Boolean random variable, which takes values true or false, people often use a different shorthand, where p(X) represents the probability that X is true and p(¬X) represents the probability that it is false.
All these conflicting shorthands may be a little confusing at times, but there is usually enough information in the context to figure out what the author means (and writing everything out in unambiguous notation usually leads to an unreadable mess).
On both discrete and continuous sample spaces, the events we describe have probability. Where they differ, in an important way, is in whether a meaningful probability is assigned to the elements of the sample space. Here is how such probabilities are usually visualized: discrete on the left, continuous on the right. In both cases, we are looking at the sample space.
On the left, we are seeing the probabilities assigned to each element of the sample space. Using this, we can easily work out the probabilities of every event as well (just add up all the probabilities of all the atomic events in the event).
However, when we look at a graph like the one on the right, describing a normal distribution, it’s important to realize that this function does not express a probability. If I ask you, under this distribution, which has the higher probability, 0 or 1, the answer is that they both have the same probability: 0. This should make intuitive sense: What is the probability of meeting somebody who is exactly 2m tall? Surely, if you measure more and more precisely, the probability of getting exactly 2m goes further and further down, converging to 0.
In short, when it comes to probability distributions on continuous spaces, the atomic events normally all have probability 0. The things that have nonzero probability are ranges of values. The probability of somebody being between 2.0m and 2.1m tall is more than 0, no matter how precisely you measure them.
So what does this curve express? Not probability but probability density. The probabilities can be retrieved by integration. For instance, the probability of getting a sample between 0 and 1 from this distribution is equal to the area highlighted in the slide. The total area between -∞ and ∞ is exactly 1.
Now that we have the basic language of probability theory in place, we can look at some of the most important concepts. We will quickly review these five.
We will use the following running example: we sample a random person from the Dutch population and we check their age and the health of their teeth (binning the results into three categories for each variable).
We want to ask questions like:
what is the probability of seeing an old person?
what is the probability that a young person has fake teeth?
does a person’s age influence the health of their teeth, or is there no relation?
The sample space is the set of the nine different pairs of values we can observe, and the event space is the powerset of that. The random variables A(ge) and T(eeth) will help us describe these events.
The joint distribution is the most important distribution. It tells us the probability of each atomic event: each event that contains a single element in our sample space.
Since we have two random variables in our example, which together capture the whole sample space, we can specify the joint distribution in a small table. The probabilities of all 9 events sum to one.
Note that p(Age = old & Teeth = healthy) refers to a single value (1/18), because we have fully specified the event. p(Age, Teeth) does not refer to a single value, because the variables are not instantiated, it represents a function of two variables, i.e. the whole table.
If we want to focus on just one random variable, all we need to do is sum over the rows or columns.
For instance, the probability that Age=old, regardless of the value of Teeth, is the probability of the event {(o,h), (o,u), (o,f)}. Because we can write these sums in the margins of our joint probability table, this process of “getting rid” of a variable is also called maginalizing out (as in “we marginalize out the variable Teeth”). The resulting distribution over the remaining variable(s) is called a marginal distribution.
This is what marginalizing looks like in symbols: we sum the joint probabilities for all values of one of the random variables, keeping the value of the other fixed.
Remember that p(X) and P(x) are both shorthand for p(X=x).
If we know that somebody is young, we know that the probability of them having false teeth must be low. This is called conditional probability: our knowledge of one random variable, given that some other variable takes some specific value. This is expressed with a vertical bar, with the known part, the conditional on the right.
The conditional probability p(X=x|Y=y) is computed taking the joint probability of (x, y) and normalising by the sum of the probabilities in the row or column corresponding to the part that’s given in the conditional.
Imagine we’re throwing darts at this table, and the probability of hitting a certain cell is the joint probability indicated in the cell. The conditional probability p(T=f|A=y) is the probability that the dart hits the (y, f) cell, given that it has hit the y row.
Note that a statement about conditional probability tells us nothing about causality. In our example age causes bad teeth, but we can express both the probability that somebody has bad teeth given that they are old (in the causal direction), and the probability that somebody is old given that they have bad teeth (in the opposite direction).
Here is what conditional probability looks like in abstract, symbolic terms. Note that the denominator is just the marginal probability
If we re-arrange the factors in the definition of the conditional probability, we get this equation, showing a kind of decomposition of the joint probability. This comes up a lot, so make a note of it.
For a specific example, the probability of seeing an old person with false teeth, is the probability that an old person would have false teeth, times the probability of seeing a old person at all. The probability that an old person has false teeth may be very high, but if the probability of seeing an old person is very small, there's still a very small probability of seeing an old person with false teeth.
Note that the same decomposition works with the reverse conditional, the probability that someone with false teeth would be old. Try it.
Here is what these concepts look like with continuous random variables (a bivariate normal distribution in this case). The joint probability distribution is represented by the point cloud in the middle. These are the values of X and Y that are likely.
Marginalizing out either variable results in a univariate normal (the red and blue distributions), the projection of the multivariate distribution onto the X and Y axes.
The conditional distribution corresponds to a vertical or horizontal slice through the joint distribution (and also results in a univariate normal).
image source: By IkamusumeFan - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=30432580
If two variables X and Y are independent, then knowing Y will not change what we know about X. More formally, the conditional distribution p(X|Y) is the same as the distribution P(X): knowing the value of Y doesn't affect our knowledge of the value of X.
If we fill in the definition of conditional probability and re-arrange the factors, we see that this implies that the joint probability of X and Y is just the product of the marginal probabilities p(X) and p(Y). Have a look at the joint probability of the age/teeth example. Are these independent random variables? What would it mean for the example if they were?
Conditional independence means that the two variables can be dependent, but their dependence is entirely explained by a third variable Z. If we condition on Z, the variables become dependent.
Conditional independence comes up a lot, and it can be tricky to wrap your head around at first, so here’s an example.
Imagine two people who work in different areas of a very big city. In principle, they work so far apart that whether or not they arrive home in time for dinner is completely independent. Knowing whether or not Alice is late for dinner tells you nothing about whether Bob is home in time for dinner. No aspect of their lives (weather, traffic) intersect in a meaningful way, except one.
Very rarely, a large monster attacks the city. In that case, all traffic shuts down and everybody is late for dinner. That means that if we know that Bob is late for dinner, there is a slight chance that it’s because of the monster, which should slightly raise the possibility that Alice is late for dinner. However, once we know whether or not the monster has attacked, knowing that Bob is late provides no additional information.
Here is another visualization, taken from Wikipedia. This one is more abstract, but sometimes, sitting down with an abstract example and trying to work through it can help a lot to train your brain to get used to complex concepts. If you're in a hurry, you can skip this one.
Imagine throwing a dart at the square on the right. We look at the probability of hitting a yellow, red or blue square (the purple ones are both red and blue). Describe these events by boolean random variables Y, R and B.
We have p(R) = 16/49 and p(B) = 18/49. These probabilities are not independent. We can work this out by counting all the squares for the event (R, B) (R, ¬B), (¬R, B) and (¬R, ¬B) and seeing if they are the product of the marginal probabilities, but we can also tell directly by looking at the picture: if we know that we've hit a blue square, there is a certain probability that that blue square is purple (i.e. also a red square). If we know that we haven't hit a blue square, there is also a certain probability that that square is red. The proportion of red inside the blue region looks different to the proportion of reds inside the non-blue region, so knowing whether we are in a blue square tells us something about how likely we are to be in a red square.
Now, let's condition on Y. Somebody tells us the dart landed in a yellow square. Now that we know this, does knowing whether the square is blue still tell us anything about whether the square is also red? Note that within the yellow block, the proportion of red within the blues is the same as the proportion of reds within the non-blues. Once we're inside the yellow block, it doesn't matter anymore whether the block is blue. The probability of red is the same either way. Conditional on the knowledge that Y=true, the probabilities of red and blue are independent.
What about when we hear that the dart has landed outside the yellow block? It's harder to see, but the proportions are 4/12 for the blue blocks and 8/25 for the nonblue. Thus the probabilities of blue and red are not conditionally independent given that Y=false.
By AzaToth at English Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=3206668
Now that we have a decent understanding of conditional probability, let's look at Bayes' rule, probably the most important application of conditional probabilities.
Bayes' rule is a solution to the inversion problem. What usually happens is that we have some idea of the mechanics of the world, and we observe some outcome, that could have happened through these mechanics in different ways. We didn't observe how it happened: that's the part that is hidden, and the part that we'd like to reason about. It's usually easy to reason about the probabilities of the outcomes given the observables (because we know the mechanics of the world) but we'd like to reverse this.
For example imagine that you call a restaurant to book a table, and nobody picks up. This is unusual, and you wonder if it means the restaurant has burned down. You can easily reason forward, from the cause to the effect. If the restaurant has burned down, you would be sure that nobody would pick up the phone. If it hasn't, you would be quite sure that somebody would pick up the phone, but not certain. This is how you would reason if you observed whether or not the restaurant burned down and had to guess whether or not the phone would be answered. You are reasoning in the causal direction, so you use your understanding of the mechanics of the world to arrive at an intuitive conclusion.
The problem is that we usually want to do backward reasoning. We observe the outcome of some event and we don't observe the cause. What we want to figure out is how to assign probabilities to the different causes. In this case, given that we observe nobody answering the phone, what is the probability that the restaurant has burned down?
In short, we need a way to “turn around” the conditional probability. If we know p(X|Y), how do we work out p(Y|X)?
To do this, we need some additional probabilities. This makes sense if you think about our example. If the restaurant has burned down, we are sure that the phone won't be answered, but if we observe that the phone wasn't answered, we can't be sure that the restaurant has burned down. We need to take into account the fact that it's very rare for a restaurant to burn down, even though it would definitely lead to this observation. We also need to take into account the probability that something else has caused the restaurant not to answer. Intuitively, you probably wouldn't jump to the conclusion that the restaurant has burned down because this is an unlikely event, and there are many other reasons for the phone not being picked up.
If the cause and effect are labeled Y (the restaurant burning down) and X (the phone going unanswered), then the marginal probabilities p(Y) and p(X) capture all this information indirectly (we'll see how in a bit). Combining them this allows us to reverse the conditional from the probability of the effect given the cause to the probability of the cause given the effect.
This is the way Bayes' rule is usually written. You can prove that this is true very simply by starting with the definition of conditional probability and using the equation in slide 119 to rewrite the numerator.
Here's the two-step proof. It probably won't convey much intuition for why Bayes' rule looks the way it does, but it should at least convince your inner mathematician that it is true.
To build a more intuitive understanding of how this formula works, let's return to the example of the monster attack. We'll focus on Alice only, and forget about Bob.
Let’s say that we observe that Alice is late for dinner (and we observe nothing else). Does this tell us anything about whether a monster has attacked the city? It doesn’t tell us much; it’s extremely rare that a monster attacks the city so it’s almost certain that Alice is late for other reasons. Still, if Alice were on time, we’d know that a monster couldn’t have attacked the city, since that would certainly make her late. So we may not know much, but we know something.
In this case it’s easy for us to work out the probability that Alice is late (the effect) given the monster attack (the cause). This is because in p(a|m), the conditional m is the cause of the observable a. The opposite is usually what we are interested in, since we have the observable and want to reason about its cause. This is where Bayes’ rule comes in.
Say that we know the probability that we observe Alice being late, given that a monster attack happened, p(a | m), is somewhere near 1. Bayes’ rule tells us how to use this to calculate the opposite conditional p(m | a). This is not near 1, because we multiply it by the marginal probability of a monster attack p(m), which is really low. We then divide by the probability of Alice being late in general p(a): the more likely Alice is to be late due to other causes, the lower the probability that it is caused by a monster attack.
If there are three possible reasons for Alice to be late: traffic, monster or snowfall. Then we can see the denominator as a sum marginalizing out the cause for Alice’s lateness. The proportion of this sum given by the middle term is the probability that Alice’s lateness is caused by a monster attack.
Consider the situation where both traffic and snowfall are far more likely than a monster attack, so p(t) and p(s) are much higher than p(m), but neither traffic nor snowfall ever cause Alice to be late, perhaps because she cycles home from work, and has a bike with good snow tires. In that case both the first and last term in the sum become zero, and despite the fact that monster attacks are really rare, we can still conclude that a monster has attacked if we notice that Alice is late for dinner.
An expectation, or expected value, is a way of expressing what you can expect to “gain” from a random process.
For example, imagine the following gamble. I roll a die and if the the number of eyes is three or fewer, you pay me that number of euros, and if it’s four or more, I pay you that number of euros.
Should you accept this gamble? Intuitively, it seems like you should. Even though you could lose money, and you are as likely to lose money as you are to gain money, in some sense, you can expect to gain more money. One way of thinking about this is what would happen if we were to repeat the gamble a large number of times. If we did that, how much would you gain, on average per roll of the die?
You can compute this by taking your gains from each possible outcome (with losses represented as negative gains), multiplying each by the probability of that outcome occurring and summing all these up. The result is that on average, you can expect to gain 1.5 euros from this gamble, even though in each individual gamble you can still lose.
We can use the sum notation from earlier in the lecture to provide a concise definition. To compute the expected value of a function f of outcomes x, under probability p, we multiply f(x) by p(x) and sum over all outcomes.
We denote the expectation with a bold or blackboard capital E. If it’s not clear which variable represents the outcome we’re summing over, or what the probability is, we can specify this in the subscript as shown (but we often leave this out to simplify the notation).
Things get a little bit more tricky if our outcomes x are continuous (i.e. real-valued numbers). In this case, our sum becomes an integral, and our probabilities become probability densities. Integrals are tricky, and it takes a lot of skill to work them out. Luckily, ion this course, you’ll never be asked to work out an integral. You just have to understand what it represents.
Moreover, most of the rules for expectations are the same whether you’re dealing with a sum-based expectation or an integral-based expectation. That means that if you never open up the E, you can just apply the rules for dealing with expectations, and simplify the function until you have the desired result.
If the function f(x) is the identity (i.e. it just returns x), then we say that the expectation is the expected value of the random variable x. For example the expected value of the number of eyes on a die is (1 + 2 + 3 + 4 + 5 + 6)/6.
question Imagine we have a loaded die. All outcomes are equally likely, except 1 which is twice as likely as each of the others. What is the expected value of x if x is the number of eyes on the side we roll with this die? The answer is 3 and 1/7 or ~3.14.
To work out the rules for manipulating expectations, all we need to do is expand the definition into a sum. What we see is that the first two rules for sums (on slide 19) also apply to expectations.
When we have constant terms, however, the rule is slightly different. The expectation of a constant value is just that constant value. That is, if I say I will roll a die and then give you 1 euro regardless of the outcome, then your expected gain is just 1 euro. With this we can show that if we have a constant term in our expectation, we can just take it outside.
In machine learning, we often have expectations that we cannot explicitly compute. In such circumstances, we usually estimate the value of the expectation by Monte Carlo estimation. This is a fancy name for a very simple idea: we just take a bunch of samples and average them.
One example is working out the expected BMI of a randomly chosen person in the Netherlands. We don’t have the data for everybody in the Netherlands, but we can easily sample, say 100 people at random, and measure their weight and height and compute their BMI. If we average all 100 BMI values, the result is is a good estimate of the true expectation.
In fact, we can prove that as our sample size goes to infinity, the difference between the true expectation and the Monte Carlo estimate goes to zero.
In formulas we write this as shown in the slides. Say that we are interested in the expectation of a function f applied to a random variable x with distribution p. We estimate this value by drawing K samples x1, …, xK from p. We then compute f(xk) for each sample xk and average the results.
Here is a famous paradox: the st. Petersburg lottery. Thinking about this for a bit may help to deepen your understanding of expectations.
If you play this game a few times (I suggest without using real money), you’ll see that the amount of money you have to pay out over a few games is relatively modest. This might inspire you to start offering the game for real. All you need to do is to charge the average amount a player makes per game. That way, if a player gets lucky and wins a lot of money, you can pay them out with the entry fees from a lot of unlucky players.
In short, you need to work out the expected payout for the game.
If you charge less than this, then it follows you will eventually make a loss. That is, a player who notices you’re undercharging can just play the game repeatedly to eventually make a gain (so long as they have sufficient capital to cover their initial losses).
The expectation is an infinite sum, because there is an infinite number of outcomes. But, remember, we shouldn’t be afraid of infinite sums. The result is 2(1/2) + 4(1/4) + 8(1/8) + … An infinite sum in which every term is one. The result is infinite.
This means that you should charge people infinitely much money. To see why this is a paradox, consider what happens if I charge less, say a million euros. If I do that, every rational player should then be willing to play the game. How much would you pay to play this game? All the money you have? Remember that in practice, there is a 50% chance that you will only make 2 euros.
Wikipedia offers some resolutions to the paradox. For my money, the main trick is that this kind of lottery is never as infinite as it looks. Let’s say that I have 1 million euros to start with. That means that if I offer the game and a run of 20 heads happens, I can’t pay out because 220 > 1 million. The actual game I offer doesn’t continue indefinitely: it stops if we see a run of 20 heads. The expected value is therefore not an infinite sum of 1s, it’s a sum of twenty 1s. This is the player’s actual expected value: 20 euros.
If I tell the player that we’ll only go to 20 heads max, they’ll quickly work out that they should not play if I charge more than 20 euros. If I don’t tell them, I’m essentially risking a 1-in-a-million chance of going from millionaire to bankrupt in order to win 20 euros. The risk is very minimal, but then so is my gain.
To finish up, we'll look at some of the most common probability distributions we'll see throughout the course. Most of these you should know already, but we'll summarize them here briefly for the sake of completeness.
The simplest is probably the Bernoulli distribution. It's any distribution with two outcomes. You can think of it as modelling the outcome of a coin flip with a (possibly) bent coin, but the outcome could also be true/false, guilty/innocent or positive/negative.
Every distribution like this, with its probabilities set to some pair of values summing to 1 is a Bernoulli distribution. To specify which Bernoulli distribution we are talking about we specify one of the probabilities by a number. The other probability is then also defined, since they must sum to one.
The numbers we use to specify which specific distribution we are talking about in a family like the Bernoulli distributions, are called the parameters, and often indicated by the greek letter theta, θ. You can think of θ as a set or a vector of number.
In the case of the Bernoulli distribution θ is just a single number between 0 and 1.
If we have more than two outcomes, but still a finite number, we can assign each a separate probability so that they sum to one. For instance, if we want to model the outcome of rolling a loaded die, it might look like this. This is called a categorical distribution. Other examples are modeling which team will win the next world cup, which child in a classroom will score the highest on a test, or what the hair color of a random person from Ireland is.
To specify a categorical distribution with n outcomes we strictly need only n-1 probabilities. We can work out the n-th probability from the knowledge that all probabilities sum to one. However, this is usually more trouble than it's worth, and instead we tend to represent categorical distributions by the slightly redundant complete set of n probabilities.
The normal distribution or Gaussian is probably the most common distribution on a continuous sample space. It is defined by this complex looking function. Don't worry about the formula too much now, we'll dig into that later. For now just remember that the curve it describes is the probability density.
Its parameters are the mean μ, which tells us where the peak is, and the variance σ2 or standard deviation σ, which tells us how widely spread out the normal distribution is.
The standard normal distribution is the specific distribution with mean 0 and variance/standard deviation 1.
The normal distribution is particularly useful for anything that has a definite scale. Consider, for instance height: people have all kinds of different heights, but if we get far enough away from the average, the probability gets so low it may as well be zero. We can say with near certainty that there are no 4 meter tall people and no 10cm tall people. If there were a hundred times as many people, that would still be true.
An example of an attribute that doesn't have such a definite scale is income. In a small population there may be millionaires but no billionaires, but if we zoom out to the population of a small country, we will see billionaires appear. In a large country will we see people with fortunes in the order of 10 billion dollars and in the whole world we will see fortunes of 100 billion dollars. In short, the largest grows exponentially with the population size.
In such cases, as we've seen, the normal distribution is not a good choice. We won't discuss them in this course, but so called fat-tailed distributions like the log-normal, Zipf or power-law distributions may be more suitable.
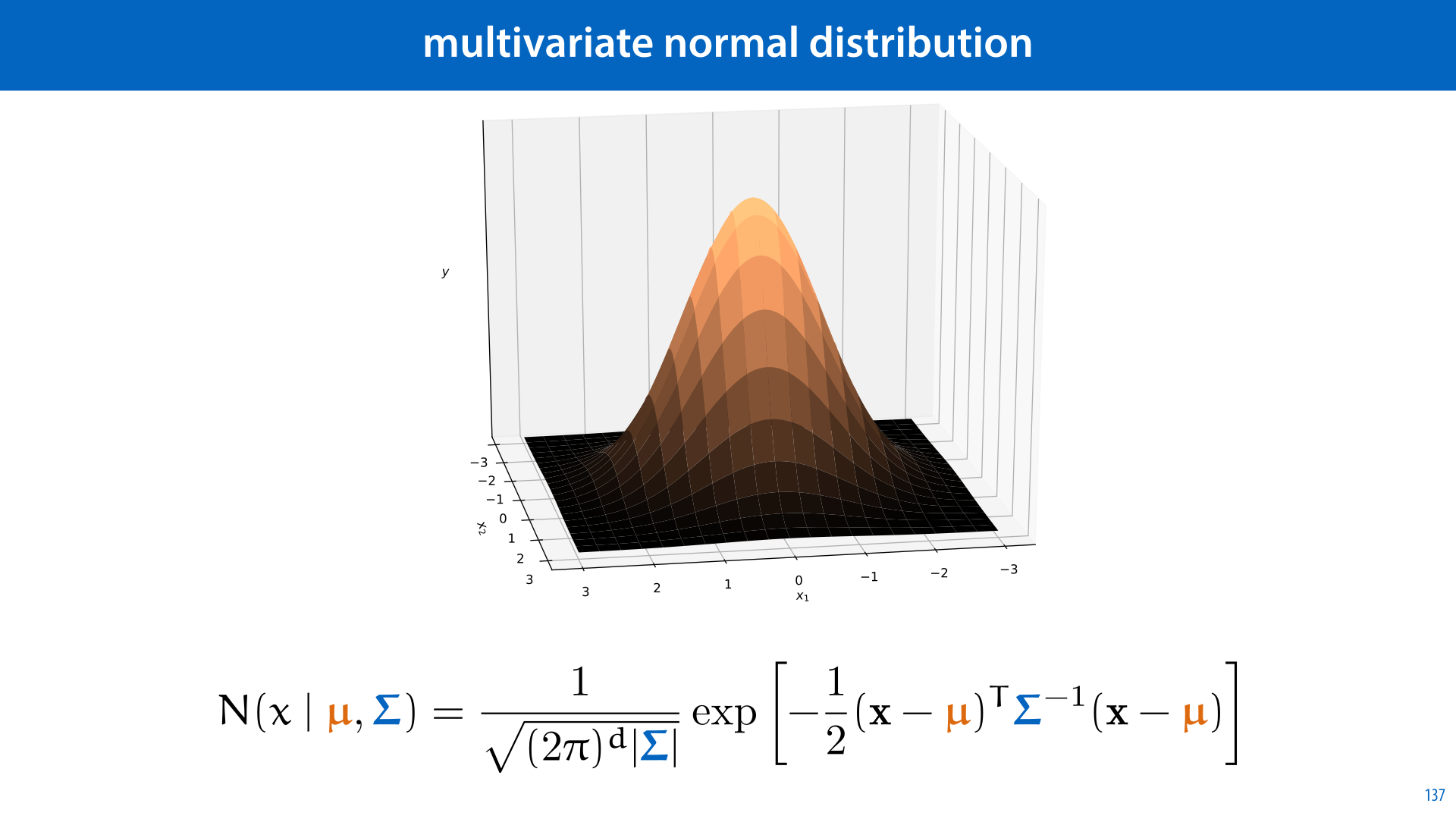
If our sample space consists of multiple numbers, for instance when we have a dataset with multiple features, we can draw this as an n-dimensional Euclidean space, like the plane shown here. A distribution over such a space can be defined by a probability density function over it, which, in the 2D case looks like a surface over the plane.
The multivariate normal distribution is an extension of the normal distribution to multiple dimensions. It takes the shape of a kind of bell over our sample space. For higher dimensions it's harder to visualize. You can think of an ellipsoidal region in space taking most of the probability mass, with the probability density decaying quickly in all directions.
Again, don't worry too much about the complicated formula for the probability density. We'll see where that comes from and what all the parts mean later. For now, just focus on the shape, and how the parameters affect that shape.
The parameters are the mean μ, a vector which provides the center, and the covariance matrix Σ, which tells us how much the probability decays in each direction.

Here is an illustration of the way the covariance matrix affects the data we get from a multivariate normal distribution. The mean is at (0, 0) in all four examples.
If the covariance is the identity matrix, we get the standard normal distribution. This is called a spherical distribution, because the variance along all axes is the same, and there is no correlation between axes, giving the data roughly spherical shape.
If we change the values on the diagonal, we stretch this sphere into an ellipse, but only along the axes. There is still no correlation: knowing the value along one axis tells us nothing about the value along the others.
If we change the off-diagonal values to positive values we get correlation. In this case having a high value along one axis makes it more likely that the value along the other axis is also high. Note that the coviarance matrix needs to be symmetric, so the value on one side of the diagonal must be the same as the value on the other side.
If the off-diagonal value is negative, we get anti-correlation. A high positive value on one axis most likely corresponds to a high negative value along the other axis.
If we have more than 2 dimensions, say n, then there are (n^2 - n)/2 possible pairs of axes between which we can define a correlation. any of these could be positive, negative or 0. This corresponds exactly to the number of values above the diagonal in an n x n matrix.